|
|
(س
ـ د)2 + ( ص ـ هـ)2 = نق2
س2 ـ 2 د س + د2 + ص2 ـ 2هـ
ص + هـ2 = نق2
س2 + ص2 ـ
2 د
س ـ
2 هـ
ص +
د2 + هـ2 ـ نق2
= صفر
بوضع
2 أ = ـ2
،
2ب = ـ2 هـ
،
جـ = د2 + هـ2 ـ نق2
تصبح المعادلة هي
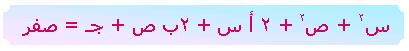
حيث 2 أ = ـ2 ، 2ب = ـ2 هـ ، جـ = د2
+ هـ2 ـ نق2
أ = ـ د ، ب = ـ هـ نق2
= د2 + هـ2 ـ جـ
|
 |
|
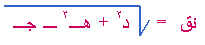
المركز هو ( د ، هـ)
|
 |
|
|
 |
|
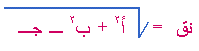( ـ أ ، ـ ب)
|
º |
|
وتتحقق في معادلة الدائرة الشروط التالية :
1. معادلة من الدرجة الثانية في س ، ص
2. معامل س2 = معامل ص2
3. خالية من الحد المشتمل على ( س ص)
4. أ2 + ب2 ـ جـ
<
صفر
ـــــــــــــــــــــــــــــ
اكتبوا لنا ملاحظاتكم واستفساراتكم
|
