|
الحد
الجبري والمقدار الجبري
تمهيد :
تعلم
أننا في الحساب نستخدم الأعداد في العمليات المختلفة (الجمع والضرب) ،
أما الجبر فهو شكل آخر للحساب نستخدم فيه الأعداد والرموز في إجراء
العمليات .
مفاهيم ومصطلحات :
انظر الأمثلة التالية :
س ، 3س ، 27 + س ، 4 ك م ـ 5 ع ل + 3 س ص ، 4 ل2 - ك - 3 ،
25ص2 - 30ص + 9 ، 5س2 ص
الحد الجبري – نسمي كل واحد من س ، 3س ، 5س2 ص
باسم الحد الجبري
.
يتكون
الحد الجبري
في أبسط حالاته من رمز ( حرف ) منفرد حيث س تعني حقاً 1س1 ،
نسمي العدد ( 1 ) إلى يمين الرمز س باسم
معامل
س ، أما العدد ( 1 ) إلى يسار الرمز س وأعلاه فهو يمثل
أُس
( قوة ) س. إن 1س1 تعني 1 × س1 . وقد اتفق علماء
الرياضيات على أنه عندما يكون معامل الرمز ( 1 ) وقوته ( 1 ) ، أن لا
نكتبها فهي تفهم مباشرة ولا حاجة لكتابته ، أما إذا كان المعامل والقوة
أكبر من ( 1 ) فيجب كتابتها لاحظ الحد 3س : إن معامل س هو ( 3 ) ، أكبر
من ( 1 ) فيجب كتابته. لاحظ الحد 3س : إن معامل س هو ( 3 ) والأس = 1 ،
وفي الحد 5س2 ص : المعامل هو (5) وقوة س = 2 وقوة ص = 1 . إن
الحد يتكون من
معامل ورمز
( أو مجموعة رموز ) مضروبة ( أو مقسومة ) في بعضها دون أي عملية جمع (
طرح ) .
المقدار الجبري :
27 + س ، 4 ك م ـ 5 ع ل + 3س ص ، 6ل2 ـ ل ـ 3 ،
25ص2 ـ 30ص + 9.
هذه عبارات جبرية تتكون من
مجموعة حدود
، إذا كان الحد يتكون من عدد فقط سمي
حداً مطلقاً
، ففي المثال 27 + س نسمي ( 27 ) الحد المطلق .
وفي العبارة ( 4 ل2 - ل - 3 ) ، ( -3 ) هي
الحد المطلق .
إذا تكونت العبارة الجبرية من حدين أو أكثر تفصل بينهما
إشارة جمع ( طرح ) فإننا نسمي العبارة الجبرية
مقداراً
جبرياً
.
تدريب :
ضع الحدود الجبرية في عمود والمقادير الجبرية في عمود آخر
|
4 ك + 3 م2 ، |
27 ع3
م2 ، |
5 س2
- 6 س + 1 ، |
| |
|
|
|
، |
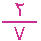ل ع2 ، |
ص3
- س3 + 2س3 - 2ص3 ،
|
| |
|
|
|
5
م 2 - 7 م + 2 . |
|
|
|
