3- نطبق القانون على الكتلة الأولى ( ك₁ ):
ش - و₁ = ش - ك₁ جـ = ك₁ ت

4- نطبق القانون على الكتلة الثانية ( ك₂ )
ش - و₂ = ش - ك₂ جـ = - ك₂ ت

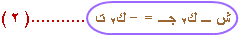5- نطرح المعادلة ( 2 ) من المعادلة ( 1 ) وينتج أن :

جـ ( ك₂ - ك₁ ) = ت ( ك₁ + ك₂ )

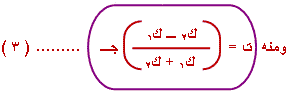
ومنه بالتعويض ك₁ = 2 كغ ، ك₂ = 4 كغ ، جـ = 9.8 م / ث²

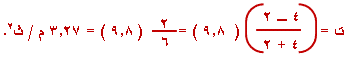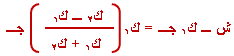
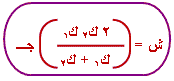
6- لإيجاد الشد في الخيط نعوض قيمة ت ( معادلة ( 3 )) في المعادلة ( 1 ):

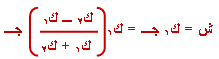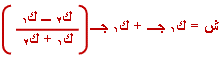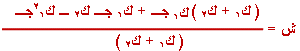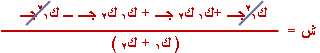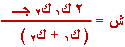وبالتعويض , ك₁= 2 كغ , ك₂= 4 كغ , جـ = 9.8  م / ث2

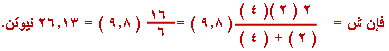ملاحظة : يمكن حساب تسارع مباشرة بحساب القوة المحصلة على النظام وقسمتها على كتلة النظام الكلية.

حالات خاصة :
1- عندما تكون ك₁= ك₂ , فإن ت = صفر ،  ش = ك₁جـ = ك₂جـ
2- عندما تكون ك₂ >> ك₁ فإن ت = جـ ، كما لو كان سقوطاً حراً ، ش @ 2 ك₁ جـ
 

اكتبوا لنا ملاحظاتكم واستفساراتكم تحرير : المدرسة العربية  www.schoolarabia.net اعداد : أسماء واصف   تاريخ التحديث 27 تموز 2002