|
ICS 353 Design & Analysis of Algorithms Fall 2007 |
|||||||
| Exams | |||||||
|
ICS 353 Design & Analysis of Algorithms Fall 2007 |
|||||||
| Exams | |||||||
![]()
Check The WebCT for solutions of these assignments.
|
Assignment Submission Rules
|
| Lateness | Penalty |
| < 5 hrs late | 5 marks |
| < 24 hrs late | 10 marks off |
| < 48 hrs late | 15 marks off |
Assignment 1: Due to Sat Mar 22nd at class time. No assignment will be accepted after due time.
Textbook Problems: Solve the following problems from chapter 1 in the textbook: 2, 5, 15, 16-(a,b), 23, 28, and 36.
External Problems:
Show that
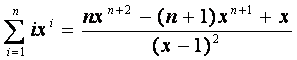
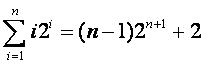
Use the above sum to prove that the average successful search time of BinarySearch algorithm on an array of size n is Θ(log n). For simplicity, you may assume that n is a power of 2.
We know that the decision tree used by the BinarySearch algorithm is an almost complete binary search tree. Prove that the reverse is not true by giving an example of an almost complete binary search tree that is not a decision tree used by the BinarySearch algorithm on any kind of array. Your tree should have the smallest possible size. Be careful.
Among InsertionSort and SelectionSort, which algorithm do you use to on an array A[1..n] that is already sorted non-increasingly and why?
Draw two strictly increasing positive functions f(x) and g(x), where xÎ[0,¥) , such that f(x) ¹ O(g(x)) and g(x) ¹ O(f(x)).
Suppose a sorting algorithm takes 3n log2 n operations to sort an array of size n, and our computer does a million operations per second. What is the largest n for which the algorithm can sort an array of size n in a day?