13.4 Some Examples of Static Equilibrium
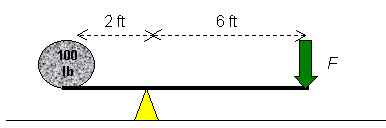
Suppose you want to lift a 100-lb rock using a light (but strong) 8-ft rod. You place the support so that it is 2 ft away from the rock and 6 ft from the end where you are pushing. What is the minimum weight you need to put on your end of the rod to hold up the rock?
Solution
This is relatively a simple problem involving static equilibrium. However this problem will be solved with the greatest details possible to make the concepts very clear and show you all the techniques of solving problems of this type. (You have more example problems listed at the "end of the section box" at the bottom).
Assume the object is in equilibrium horizontally as shown in the figure and find just the value of F to maintain this equilibrium, but how?
Click on each item below to expand/collapse:
|
||||||||||||||||||||||||||||||||||||
