Example 13.4.2
Suppose a mass m is supported by two ropes, as shown below. One rope extends horizontally from the wall, and the other rope goes to the ceiling at an angle q from the vertical. Calculate the tension in each rope.
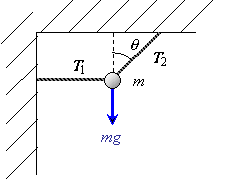
Example 13.4.2
Suppose a mass m is supported by two ropes, as shown below. One rope extends horizontally from the wall, and the other rope goes to the ceiling at an angle q from the vertical. Calculate the tension in each rope.
