Summary of Chapter 17
![]()
1.
Wave is the motion of a disturbance.
2.
There are two (2) types of
waves:
Transverse Waves: The particles of the disturbed medium
move perpendicular to the wave velocity
(example: waves on a
string).
Longitudinal Waves: The particles of the disturbed medium
move parallel to the wave velocity
(example: sound waves).
3.
For a sinusoidal
wave the transverse displacement y at position x at time
t is given by
![]()
This equation represents the displacement of the particles of the
medium as a function of x and t.
where ym is the amplitude
of the wave in (m), k is the wave number
in (rad/m), w is the angular frequency in (rad/s).
![]()
The expression (![]() ) is called the phase angle and its units is radians.
) is called the phase angle and its units is radians.
The plus (+)
sign means the wave is traveling to the left.
The minus (-) sign means the wave is traveling to the right.
A
wave is said to be stationary if is time
independent, i.e., y (x) = f (x).
A
travelling wave can be longitudinal or transverse.
Ø The transverse velovity (the velocity of
the particles) is given by ;
![]()
The maximum transverse
velocity is umax = ym w (m/s)
Ø The transverse acceleration (the
acceleration of the particles) is given by;
![]()
![]()
The maximum transverse acceleration is amax = ym w2
(m/s2)
4.
The
speed of the wave is constant
and given by ![]()
The wavelength l is the distance between two
successive maxima (crests) or minima (throughs) or any two identical points on
the wave.
The frequency of the wave is
also related to the period T in (s) by ![]()
5.
In
the case of a stretched string
as in the figure, the wave speed is given by:
![]()

where T
is the tension in the string in (N), m is the
linear mass density (kg/m) and v is the speed
of the wave (m/s).
6.
The
power transmitted by a harmonic wave moving in a stretched string is given by; ![]() with
units of Watt
with
units of Watt
7.
Superposition of Waves
Suppose two waves y1
(x,t) and y2(x,t) are moving through a medium, the total
displacement of the medium y(x,t) at a point x at time t
is
![]()
y(x,t)
is called the resultant
wave.
8.
Interference of Waves
The net displacement of two equal sinusoidal waves
(the resultant) traveling in the same
direction equals the algebraic sum of the displacement of the two waves.
y1 = ym sin(k x - w t)
y2
= ym sin(k x - w t + f)
The
resultant wave function is y = y1 + y2 = [2 ym
cos f/2] sin(k x - w t + f/2)
Amplitude of the resultant
wave
![]()
3 Cases:
a)
The amplitude of the
resultant wave is maximum (constructive interference) when f = 0, 2p, 4p, 6p,
b)
The amplitude of the
resultant wave is zero (destructive interference) when f = p, 3p, 5p,
c) Intermediate
interference when 0 < f
< p etc, ..
9.
Standing Waves
If
two equal sinusoidal waves travel in opposite
directions along a stretched string, their interference with each other produce
a standing wave.
y1 = ym
sin(k x - w t) and y2 = ym sin(k x + w t)
y = y1 + y2
=[ 2 ym sin(k x)] cos(w t)

2
Cases:
a)
position of the nodes or minimum
amplitude:
kx = np, for
n = 0, 1, 2, 3,
but k
= 2p/l
Þ x = l/2, l, 3l/2, = nl/2
for n = 0, 1, 2, 3,
b)
position of the anti-nodes
or maximum
amplitude:
k x = p/2, 3p/2, 5p/2, = np/2 for n = 0, 1, 2, 3,
but k
= 2p/l
Þ x = l/4, 3l/4, 5l/4, = nl/4
for n = 1, 3, 5
A standing Wave 
10.
Standing Waves and Resonance
in a stretched string
In
the case of a stretched string resonance occur and standing wave patterns are
formed at certain freqencies called resonant
frequencies.
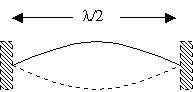 The
standing wave patterns in the case of a stretched string are as follows:
The
standing wave patterns in the case of a stretched string are as follows:
Fundamental mode
or first harmonic
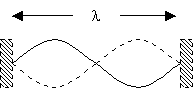
Second harmonic
The relation between the wavelength (l) and the length of the string (L) is:
![]() or
or
![]() for n = 1, 2, 3,
for n = 1, 2, 3,
As you can see from the figures, n represents the number of
loops or segments.
The resonant frequencies are given by (v = l f)
![]() for n = 1, 2, 3,
for n = 1, 2, 3,
In this case we can either fix
the tension and varie the frequency to obtain the various harmonics
or fix the frequency
and change the tension to obtain the various
harmonics.
This latter case was done in the Phys. 102 lab. (Standing waves in a string).