|
تبسيط
المعادلات الجبرية
بغرض حل المعادلات الجبرية ، نقوم
باستخدام القوانين والعمليات الحسابية الأساسية .
 نبدأ بتبسيط المقادير الجبرية أو العددية الموضوعة
ضمن أقواس .
نبدأ بتبسيط المقادير الجبرية أو العددية الموضوعة
ضمن أقواس .
 نبسط المغيرات والأعداد المرفوعة لقوة ما (لأس ما)
.
نبسط المغيرات والأعداد المرفوعة لقوة ما (لأس ما)
.
 نُجري بالترتيب من اليمين إلى اليسار عمليات الضرب
والقسمة .
نُجري بالترتيب من اليمين إلى اليسار عمليات الضرب
والقسمة .
 ثم نُجري بالترتيب من اليمين إلى اليسار عمليات
الجمع والطرح .
ثم نُجري بالترتيب من اليمين إلى اليسار عمليات
الجمع والطرح .
تنبيه
 بإمكاننا دمج الحدود المتشابهة . بمعنى يُمكننا
جمع أو طرح المتغيرات المتشابهة (نفس الرمز ونفس الأس)
بإمكاننا دمج الحدود المتشابهة . بمعنى يُمكننا
جمع أو طرح المتغيرات المتشابهة (نفس الرمز ونفس الأس)
2 س + 4 س
تبسط إلى
6 س
13 – 7 + 3
تبسط إلى
9
2 س + 3 ص + 6 + 5 س + 4 ص + 9
تبسط إلى
7 س + 7 ص + 15
 بإمكاننا إضافة أي مقدار عددي إلى طرفي
المعادلة
بإمكاننا إضافة أي مقدار عددي إلى طرفي
المعادلة
س – 4 = 8
(س – 4) + 4 = 8 +
4
 بإمكاننا طرح أي مقدار عددي من طرفي
المعادلة
بإمكاننا طرح أي مقدار عددي من طرفي
المعادلة
س + 4 = 8
(س + 4) –
4
= 8 –
4
 بإمكاننا ضرب طرفي المعادلة بأي مقدار عددي عدا الصفر
بإمكاننا ضرب طرفي المعادلة بأي مقدار عددي عدا الصفر
|
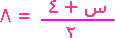 |
¬ |
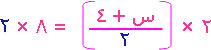 |
 بإمكاننا قسمة طرفي المعادلة على أي مقدار عددي
عدا الصفر بإمكاننا قسمة طرفي المعادلة على أي مقدار عددي
عدا الصفر
7 س = 14
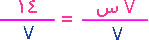
مثل
:
جد حلاً للمعادلة 2 × (س + 1 + 4) = 20
الطرف الأيسر للمعادلة مكتوب بأبسط صورة
(العدد 20)
نأخذ الطرف الأيمن ونتسلسل في عمليات
التبسط
2 × (س + 1 + 4) = 2 × (س + 5)
خاصية التوزيع / الضرب
= 2 × س + 2 × 5
= 2 س
+ 10
وهكذا تصبح المعادلة
2 س + 10 = 20
نطرح العدد 10 من طرفي المعادلة
2 س + 10 – 10 = 20 – 10
2 س = 10
تقسم طرفي المعادلة على العدد 2
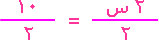
س = 5
نقول
س = 5 هو حل للمعادلة
2 × (س + 1 + 4) = 20
ونتحقق من الحل بتعويض قيمة
س
2 × (5
+ 1 + 4) = 20
2 × (10) = 20
2 × 10 = 20
20 = 20
وهكذا فإن حلنا صحيح . |


