ICS 103: Computer Programming in C
Handout-11
Topic: Recursive
Functions
Instructor:
M. Waheed Aslam.
Objective:
·
To know about importance, working & use of recursive
functions.
What is Recursive
Function?
·
Functions
which call themselves repeatedly until some condition is met and then stops
calling and returns to the main program.
A recursive
function has two parts:
(1)
Base
case (stopping condition)
(2) General case (recursive
step: which must always get closer to base case from one invocation to
another.)
e.g.,
![]() 1 for n = 0 (base case)
1 for n = 0 (base case)
n!=
n * (n-1)! for n
> 0 (general case)
A recursive solution always needs a
stopping condition to prevent an infinite loop and we achieve it by using base
case.
Simple Example: Power
function
/* Objective: To
see how recursive functions are coded and
how they
are called from main function
*/
#include<stdio.h>
power(int x, int y) // Function
definition
{
if(y==0) return 1; /*
base case */
else
return (x*power(x,y-1));
/*general case */
}
void main( )
{ int n1,n2, result_power; //
variable declaration
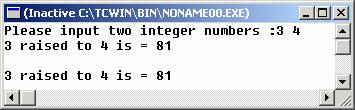
printf("Please input two integer numbers :");
scanf("%d %d", &n1, &n2); // input
result_power = power(n1,
n2); // function call
printf("%d raised to %d is =
%d\n\n",n1,n2,result_power);
printf("%d raised to %d is = %d",n1,n2,power(n1,
n2)); // function call here also
} // end of calling main function
Sample Output :
·
Any problem which we can solve using recursion,
we can also solve that problem using iteration.
·
Generally,
a recursive solution is slightly less efficient, in terms of computer time,
than an iterative one because of the overhead for the extra function calls.
·
In
many instances, however, recursion enables us to specify a natural, simple
solution to a problem that otherwise would be difficult to solve.
·
For
this reason, recursion is an important and powerful tool in problem solving and
programming.
·
Recursion
is used widely in solving problems that are not numeric, such as proving
mathematical theorems, writing compilers, and in searching and sorting algorithms.
·
In iterative method we use for, while, do-while for
achieving iteration for problem solving.
·
In recursive method of problem solving we
replace for, while, do-while statements
by if statement that selects between the recursive case and the base case (i.e.,
terminating condition).
·
In recursion, successive function call values
are stored in stack and accessed in LIFO.
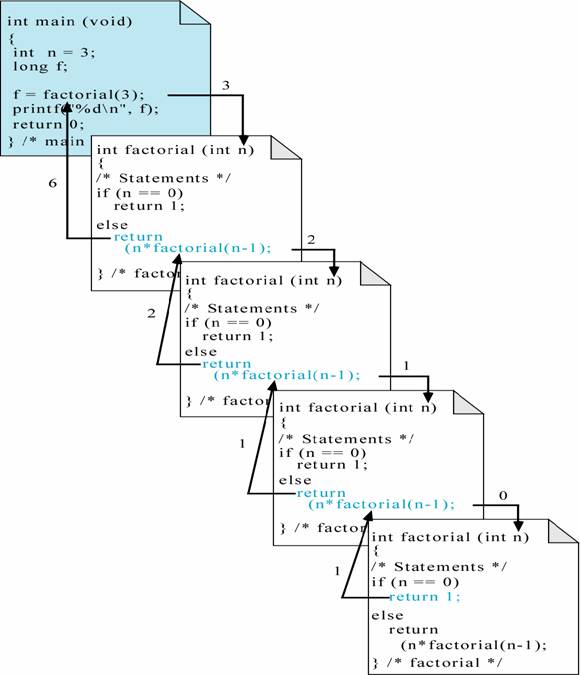
Examples #1:
|
/*compute n! using a
recursive definition*/ |
/*iterative solutions computes n! for n >=0*/ |
|
int
factorial (int n) { if (n == 0) return 1; else return( n * factorial (n-1)); } |
int
factorial (int n) { int
i, product=1; for
(i=n; i>1; --i) /* n * (n-1)
* (n-2)…*/ product=product *i; return (product); } |
Example #2: Power function: base exp.
One way to do the calculation is:
base
exp= base * base * base * … * base
(exp times).
A more compact way is:
base exp = base * base exp-1
In this case the stopping condition (the
base case) occurs when exp=0. Since any number raised
to the 0 power is 1, we have the following situation:
![]() 1 for exp=0 (base case)
1 for exp=0 (base case)
base exp
=
base* base exp-1
for exp > 0 (General Recursive case).
Implementation of Power Function:
Recursive
|
Iterative
|
|
#include <stdio.h> //To use scanf
and printf double power(double base, int exp) { if ( exp
== 0) return
(1); else return (base * power(base, exp -1)); } |
#include<stdio.h> //To use scanf
and printf double power(double base, int exp) { int count;double product;
product=base;
for ( count = exp-1; count >0; count --)
product = product * base; return ( product); } //
OR – see below |
|
|
#include<stdio.h>
//To use
scanf // and printf double
power(double base, int exp) {
double p=1; while(exp !=0) { p *= base; exp --;} return p; } |
The main function to be used with
the above power functions could be as follows:
void
main( )
{ double base; int
exp;
printf("Please input two
numbers,\n");
printf("the first for the base as double and\n");
printf("the second for the exponent as integer
number:\n");
scanf("%lf %d", &base, &exp); // input
printf("%lf raised to %d is =
%lf",base,exp,power(base, exp));
} // end of calling main function
Sample Output

Example #3: Fibonacci sequence:
The Fibonacci numbers are a sequence of numbers
that have many varied uses
the Fibonacci sequence 0, 1, 1,2,3,5,8,13,21,34
Fibonacci number Begins with the term 0 and 1 and
has the property that each succeeding term is the sum of the two preceding terms.
Fibonacci(0) is 0
Fibonacci (1) is 1
Fibonacci n is Fibonacci n-2 + Fibonacci n-1, for
n >2
This is defined recursively as:
f0 = 0, f1
= 1 fi+1 = fi
+ fi-1 for i =1,2, …
i.e. except for f0
and f1, every element is the sum of its previous two elements:
0,
1, 1, 3, 5, ...
The following functions implements
computing the nth Fibonacci number:
Iterative
Solution
|
Recursive
Solution
|
|
#include<stdio.h> //To
use scanf and printf int
fibonacci (int n) { int
i,sum1=0, sum2=1, sum; if (n<=1) return n; else {
for (i=2; i<=n; i++) { sum=sum1+sum2; sum1=sum2; sum2=sum; } return sum; } } |
#include<stdio.h>
//To use scanf and printf int
fibonacci(int n) { if (n<=1) return n; else return (fibonacci(n-1) + fibonacci(n-2)); } |
void main( )// main function
for fibonacci functions
{ int n, result;
printf("Please enter n to find the nth Fibonacci
number:");
scanf("%d", &n); // input
result=fibonacci(n);
printf("\nThe fibonacci number for n = %d is
%d\n",n,result);
} //
Sample Output :

·
In
recursive function call, Dynamic memory allocation occurs at run
time.
·
With
each function call, an activation record contains the state of a given
function, that is, the address of the current instruction and the values of all
the local variables, is created and pushed on the run-time stack.
·
Each
time a function calls itself, an activation record is
created and pushed on the run-time stack.
·
The
first call thus appears at the bottom of the sack.
·
The
last call (the base case) appears at the top of the stack.
·
At
that time the top activation record is popped from the stack and the function
returns its first value.
·
The
process continues until all activation records are popped from the stack,
at which time the recursion stops.