Introduction to graphs
Objectives of this lecture
q Introduce the concept of graphs and learn some of its
terminologies
q Study various method of representing graph on the
computer
What is a graph?
q A graph G consists of a set V, whose members are called the vertices of G, together with a set E of pairs of distinct vertices
from V, called the edges of G.
q If the pairs in the set E are
unordered, G is called an undirected graph; otherwise
it is called a directed graph. The term directed graph is often shortened to digraph, and the unqualified term graph usually means undirected graph.
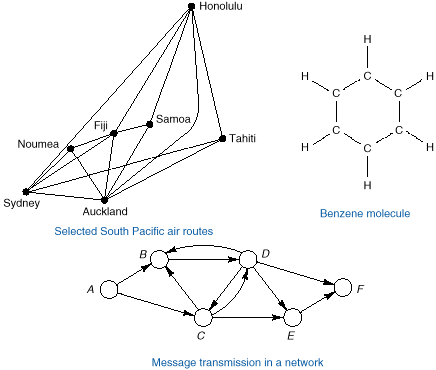
q The following figure shows some examples of graphs.
Notice that unlike
lists and trees
q The nodes are labeled, so that we can refer to them by
name.
q Each node may have multiple edges connected to it.
q Graphs don't have a unique start node.
q Graphs don't necessarily have a unique end node.
Why do we need graphs?
q Graphs find their importance in many types of
applications, Some examples are:
Ø
In a telephone system,
finding the least congested route between two phones, given connections between
switching stations.
Ø
On the web, determine if
there is a way to get to one page from another, just by following normal links.
Ø
While driving, find the
shortest path from one city to another.
Ø
As a traveling
salesperson who needs to visit a number of cities, find the shortest path that
includes all the cities.
Ø
Determine an ordering of
courses so that you always take prerequisite courses first.
Further terminologies
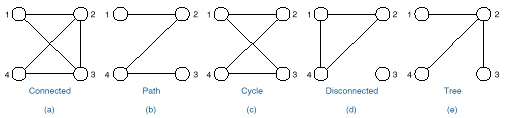
q Two vertices in an undirected graph are called adjacent if there is an edge from the first
to the second.
q A path is a sequence of distinct
vertices, each adjacent to the next.
q A cycle is a path containing at
least three vertices such that the last vertex on the path is adjacent to the
first.
q A graph is called connected if there
is a path from any vertex to any other vertex.
q A free tree is defined as a connected undirected graph with
q no cycles.
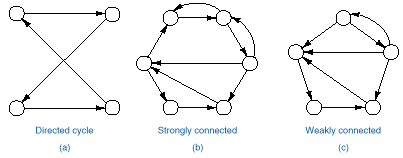
q In a directed graph a path or a cycle means always moving in the direction indicated by the
arrows. Such a path (cycle) is called a directed path (cycle).
q A directed graph is called strongly connected if there is a directed
path from any vertex to any other vertex. If we suppress the direction of the
edges and the resulting undirected graph is connected, we call the directed
graph weakly connected.
q The valence of a vertex is the
number of edges on which it lies, hence also the number of vertices adjacent to
it.
Representation of Graphs:
q There are several methods of representing graph as an
abstract data type. These methods
include using sets, tables, list, etc.
1. Adjacency table method
q In this implementation, a two dimensional array of Boolean
is used. Assuming that the vertices are
indexed with integers 0...n-1, where n denotes the number
of nodes, then the following shows the declaration required:
typedef Boolean AdjacencyTable[MAXVERTEX][MAXVERTEX]; typedef struct graph { int n; /* number of vertices in the graph */ AdjacencyTable A;} Graph;
q Notice that the adjacency table A has a natural
representation that A[v][w] is true if v is adjacent to w.
q If the graph is directed, A[v][w] is interpreted as the edge from v to w.
q If the graph is undirected, then the adjacency table
is symmetric. i.e. A[v][w] = A[w][v] for all v &w.
2. Adjacency list
q Another way to represent graph is by representing the
set of vertices as a list and for each vertex, the set of vertices adjacent to
it is also represented as a list.
q This can be implemented in at least three different
ways.
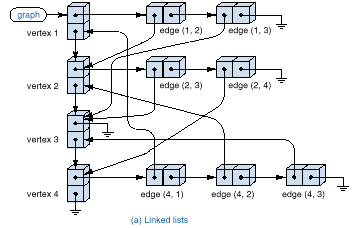
(a). Linked list
q In this case, both the vertices and adjacency list are
represented as linked lists. This has
the greatest flexibility.
typedef struct vertex Vertex;typedef struct edge Edge; struct vertex { Edge *firstedge; /* start of the adjacency list */ Vertex *nextvertex; /* next vertex on the linked list */}; struct edge { Vertex *endpoint; /* vertex to which the edge points */ Edge *nextedge; /* next edge on the adjacency list */}; typedef Vertex *Graph; /* header for the list of vertices */
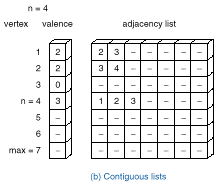
(b). Contiguous implementation
q Although the linked list implementation above is
flexible, many of the graph algorithms require random access which it cannot
provide. Therefore, the following
contiguous implementation is often better.
typedef int AdjacencyList[MAXVERTEX]; typedef struct graph { int n; /* number of vertices in the graph */ int valence[MAXVERTEX]; AdjacencyList A[MAXVERTEX];} Graph;
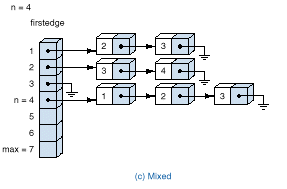
(c). Mixed implementation:
q The final implementation uses a contiguous list for
the vertices and linked list for the adjacency lists.
typedef struct edge { Vertex endpoint; struct edge *nextedge;} Edge; typedef struct graph { int n; /* number of vertices in the graph */ Edge *firstedge[MAXVERTEX];} Graph;
q Note: many
applications require not only the adjacency information specified in the
various implementation, but also further information specific to the
vertex. This can be included as additional
fields in the appropriate declarations.
Exercises:
Try
Exercises E1-E3, of pages 530-531
of your book.