AVL Trees
Objectives of this lecture
q Learn about AVL tree and its
operations
q Learn why AVL tree is better
than a random BST
What is an AVL tree?
q The function for building a
nearly balanced BST (Lecture 20) is very useful when we have a sorted list.
q It can even be used to
restore balance to an unbalanced BST
q However, it has very limited
use because it assumes that the data is fixed.
In many applications, insertion and deletion is a continuous process.
q AVL method is better, for it
ensures that a BST is nearly balanced at all times.
q AVL tree was discovered by
two Russian mathematicians, Adelson-Veslkii and Landis, hence the name AVL.
q An AVL tree is a BST in
which the height of the left and right subtrees of the root differ by at most 1 and in which the left and
right subtees are again AVL trees.
q Each node of an AVL tree is
associated with one more field, the balanced factor. This could be left higher, equal height, or right higher.
q Thus, the declaration of
TreeNode is modified as follws:
typedef
enum BalanceFactor{ LH, EQ, RH }BalanceFactor;
typedef
struct node {TreeEntry entry;
BalanceFactor bf;
struct node *left;
struct node *right;
} TreeNode.
q The following figures show
examples of AVL and non-AVL trees.
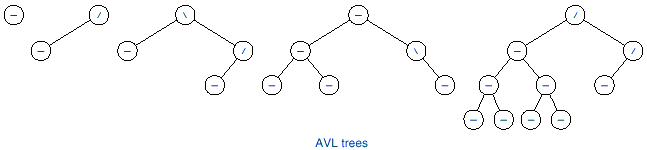
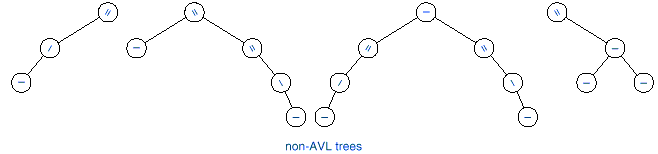
Notice that /, -, and \ are used in the figures to represent be left higher, equal
height, and right higher
Insertion
q A node is inserted into an
AVL tree using the normal insert function for BST. After the insertion, the balance factor of the resulting tree has
to be updated and if necessary re-structured to restore its AVL status.
q There are three cases:
1.
The
insertion does not change the height of the subtree the root is not affected,
only need to change the balance factor of the subtree
2.
The
insertion increased the height of the shorter (or equal) subtree need to
change the balance factor of both the root and the subtree.
3.
The
insertion increased the height of the taller subtree the tree is no longer an
AVL. It has to be restructured to make
it into AVL.
Example: The following demonstrates simple insertion (cases 1 and 2) into an AVL tree.
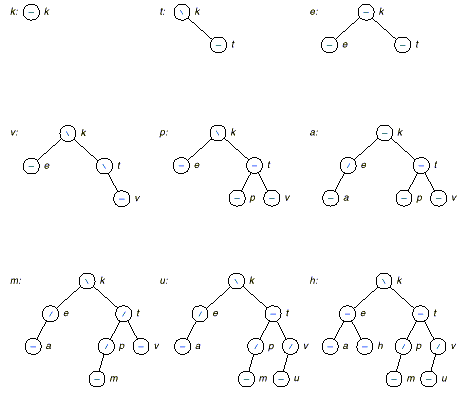
Implementation.
q We shall develop two
functions, LeftBalance and RightBalance, that restore balance when
a node is inserted on a left and right subtree
q Assuming these functions,
the insertion function can be coded as:
/* InsertAVL: insert
newnode in AVL tree starting at the root.
Pre: The root of the AVL tree is pointed by root,
and newnode is a new
node to be inserted into the tree.
Post: newnode has been
inserted into the AVL tree with taller equal to
TRUE if the height of the tree has
increased, FALSE otherwise.
Uses: InsertAVL
recursively, RightBalance, LeftBalance.
*/
TreeNode
*InsertAVL(TreeNode *root, TreeNode *newnode,
Boolean *taller)
{ if (!root) {
root = newnode;
root->left = root->right = NULL;
root->bf = EH;
*taller = TRUE;
} else if (EQ(newnode->entry.key,
root->entry.key)) {
Error("Duplicate key is not
allowed in AVL tree.");
} else if (LT(newnode->entry.key,
root->entry.key)) {
root->left =
InsertAVL(root->left, newnode, taller);
if (*taller) /* Left subtree is taller. */
switch(root->bf) {
case LH: /* Node was left high. */
root = LeftBalance(root,
taller); break;
case EH:
root->bf = LH; break;
/* Node is now left high. */
case RH:
root->bf = EH; /* Node now has balanced height.*/
*taller = FALSE; break;
}
} else {
root->right =
InsertAVL(root->right, newnode, taller);
if (*taller) /* Right subtree is taller. */
switch(root->bf) {
case LH:
root->bf = EH; /* Node now has balanced height.*/
*taller = FALSE; break;
case EH:
root->bf = RH;
break; /* Node is right high. */
case RH: /* Node was right
high. */
root = RightBalance(root,
taller); break;
}
}
return root; }
Balance
restoration
q When a new node has been inserted
into the taller subtree, then we must rebuild part of the tree to restore its
balance.
q Let the taller subtree be
the right subtree, r be the root of the tree and x be the root of the right subtree
q Then there are two cases to
consider:
1. Right Higher: The insertion makes the
right of x to be higher
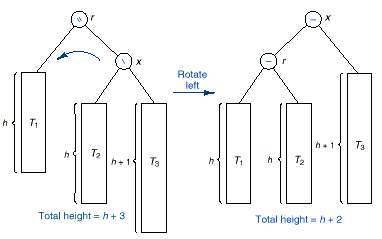
q In this case we need to
perform a left rotation.
q The node x is rotated up to become the
new root and r becomes its left child.
q The left subtree of x becomes the right subtree
of r.
q The following code
implements left rotation.
/*
RotateLeft: rotate a binary tree to the left.
Pre: p is the root of the nonempty AVL subtree
being rotated, and its
right child is nonempty.
Post:
The right child of p becomes the new p. The old p becomes the
left child of the new p.
*/
TreeNode
*RotateLeft(TreeNode *p)
{ TreeNode *rightchild = p;
if (!p)
Error("Not possible to rotate
an empty tree in RotateLeft.");
else if (!p->right)
Error("Not possible to make an
empty subtree the root.");
else {
rightchild = p->right;
p->right = rightchild->left;
rightchild->left = p;
}
return rightchild;
}
q Notice that a right
rotation is the
reverse of the left rotation above.
2. Left Higher: The insertion makes the left of
x to be higher
q This is slightly more
difficult. It is necessary to access
the node, w, on the left of x.
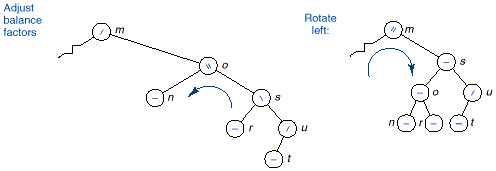
q The restoration involves double
rotations as
shown in the following figure:
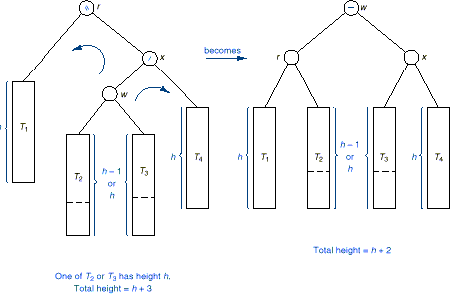
q First we perform a right
rotate and then
a left rotation on w.
q Notice that the updated
balance factor of x and r depends on the initial balance factor or w as shown by the following
table.
|
old w |
new r |
new x |
|
- |
- |
- |
|
/ |
- |
\ |
|
\ |
/ |
- |
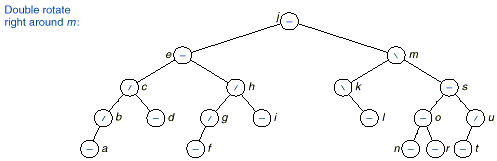
Example:
q The following figure shows
an example of insertion requiring simple and double rotations.
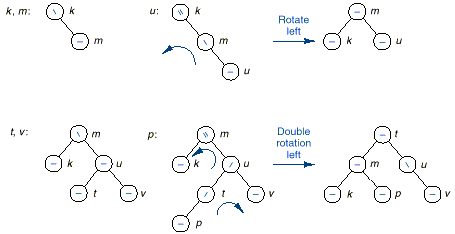
q The following implements the
function RightBalance.
/*
RightBalance: right balance a binary tree.
Pre: A node of an AVL tree has become doubly
unbalanced to the right.
Post:
The AVL properties have been restored.
Uses:
RotateRight, RotateLeft.
*/
TreeNode
*RightBalance(TreeNode *root, Boolean *taller)
{ TreeNode *rs = root->right; /* right subtree of root*/
TreeNode *ls; /* left subtree
of right subtree */
switch(rs->bf) {
case RH:
root->bf = rs->bf = EH;
root = RotateLeft(root); /* single rotation left */
*taller = FALSE;
break;
case EH:
Error("Tree is already
balanced");
break;
case LH: /* double rotation left */
ls = rs->left;
switch(ls->bf) {
case RH:
root->bf = LH;
rs->bf = EH;
break;
case EH:
root->bf = rs->bf =
EH;
break;
case LH:
root->bf = EH;
rs->bf = RH;
break;
}
ls->bf = EH;
root->right = RotateRight(rs);
root = RotateLeft(root);
*taller = FALSE;
}
return root;
}
q If the insertion is on the
left subtree of the root, then the restoration process is similar and is left
as an exercise.
Analysis:
q Notice that insertion of a
new node into an AVL tree involves at most, only one (simple or double)
rotation
q Moreover, most of the
insertions do not involve any rotations.
q Thus, the height of the tree
is kept short at a little expense.
q Clearly, the operations on
insertion, and retrieval would be more efficient when compared with a random
BST.
Deletion of a Node:
q Deletion of a node from an
AVL tree can change its AVL status, thus again the balance has to be restored.
q The process of restoration
in this case is slightly more difficult and we shall only explain it by
example.
q It involves the restoration
of the parent node (parent of the deleted node).
q This however, could change
the balance of the grandparent, etc.
q Thus, the restoration
process has to propagate up until either the root is reached or until a node
whose balance has not been affected is reached.
q The following figure
demonstrates the deletion process.
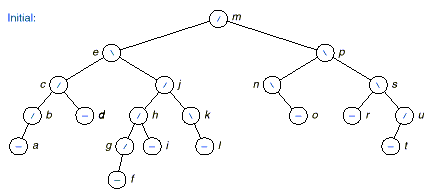
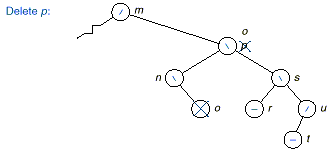
Exercises:
Implement
the LeftBalance function.
Try
Exercises E1-E5, of pages 436-437
of your book.