|
The following questions are practice problems associated with the lecture material on the subject of Boolean Algebra. These "bigger problems" have appeared on past exams in this course; variation of them will be found on your first exam in a few weeks. Is best to solve these algebracic derivations with paper and pencil, rather than by guessing and pushing buttons, by the way!
(Go back to homepage.)
-
Which of the following relationships represents the dual of the Boolean property x + x' = 1? (Note: * = AND, + = OR)
- x'* x = 1
- x * x'= 1
- x + x'= 0
- x * x'= 0
- x'* x = 0
-
An equivalent representation for the Boolean expression
A' + 1 is
- A
- A'
- 1
- 0
-
Simplification of the Boolean expression
(A+B+C)(D+E)' + (A+B+C)(D+E) yields which of the following results?
- A + B + C
- D + E
- A'B'C'
- D'E'
- None of the above
-
Given the function F(A,B,X,Y) = AB + X'Y, the most simplified Boolean representation for F' is
- (AB)' + (X'Y)
- A'B' + XY'
- (A'+ B')(X + Y')
- (AB + X'Y)'
- (AB)'(X'Y)'
-
An equivalent representation for the Boolean expression
A + A' is
- 1
- 0
- A
- A'
- A'*A
-
Simplification of the Boolean expression
AB + ABC + ABCD + ABCDE + ABCDEF yields which of the following results?
- ABCDEF
- AB
- AB + CD + EF
- A + B + C + D + E + F
- A + B(C+D(E+F))
-
Given the function F(X,Y,Z) = XZ + Z(X'+ XY), the equivalent, most simplified Boolean representation for F is
- Z + YZ
- Z + XYZ
- XZ
- X + YZ
- none of the above
-
Given that F = A'B'+ C'+ D'+ E', which of the following represent the correct expression for F'?
- F'= A+B+C+D+E
- F'= ABCDE
- F'= AB(C+D+E)
- F'= AB+C'+D'+E'
- F'= (A+B)CDE
-
Simplification of the Boolean expression (A+B+C) + (A+B+C)'(D+E) yields which of the following results?
- A + B + C
- D + E
- A'B'C'
- D'E'
- A+B+C+D+E
-
Which of the following Boolean functions is algebraically complete?
- F = xy
- F = x + y
- F = x'
- F = xy + yz
- F = x + y'
-
Which of the following relationships represents the dual of the Boolean property x + x'y = x + y Choose the best answer.
- x'(x + y') = x'y'
- x(x'y) = xy
- x*x' + y = xy
- x'(xy') = x'y'
- x(x' + y) = xy
-
Simplification of the Boolean expression
(A + B)'(C + D + E)' + (A + B)' yields which of the following results?
- A + B
- A'B'
- C + D + E
- C'D'E'
- A"B'C'D'E'
-
Given that F = (A + B'+ C)(D + E), which of the following represents the only correct expression for F'?
- F' = A'BC'+ D'+ E'
- F' = AB'C + DE
- F' = (A'+ B + C')(D'+ E')
- F' = A'BC' + D'E'
- F' = (A + B'+ C)(D'+ E')
-
Simplification of the Boolean expression AB + A(BC)' yields which of following results?
- A
- BC
- B
- AB
- (BC)'
-
Simplifing (AB)' + A'B to most basic form yields which of the following expressions?
- A'
- B'
- A+B
- B
- (AB)'
-
Which of the following Boolean functions is not algebraically complete?
- (xy)'
- (x+y)'
- xy + yz
- xy + yz'
- x'+ y'
|
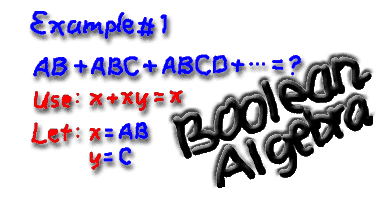 Copyright © Dean Johnson 2000
(johnson@wmich.edu)
Copyright © Dean Johnson 2000
(johnson@wmich.edu)