You, the expert, will decide, "this is an energy problem," or, "this is a Newton 2 problem." A novice is more likely to decide, "this is a pulley problem," or, "this is a baseball problem." The novice concentrates on the surface features of the problem while you concentrate on the underlying principle. You, an expert problem solver, will answer these questions, play around (briefly) with the problem, and make drawings and sketches (either in your mind, or even better, on paper) before writing down formulas and plugging in numbers. A novice problem solver, on the other hand, will try to write down equations and plug in numbers as soon as possible. A novice will make many more mistakes than you will when you become an expert.
In a physics course it's important to remember a couple of things about physicists and physics professors:
- A physicist seeks those problems that can be modeled or represented by
a picture or diagram. Almost any problem you encounter in a
physics course can be described with a drawing. Such a drawing often
contains or suggests the solution to the problem.
- A physicist seeks to find unifying principles that can be expressed mathematically and that can be applied to broad classes of physical situations. Your physics text book contains many specific formulas, but you must understand the broader Laws of Nature in order to grasp the general overview of physics. This broad understanding is vital if you are to solve problems that may include several different principles and that may use several different formulas. Virtually all specific formulas in physics are combinations of basic laws.
General outline of how to approach a physics problem:
- Read the problem. Look up the meanings of any terms that you do
not know. Answer for yourself the question, "What's this
about?" Make sure you understand what is being asked, what the
question is. It is very helpful if you reexpress the problem in your own
words or if you tell a friend what the problem is about.
- Make a drawing of the problem. Even a poor drawing can be
helpful, but for a truly good drawing include the following:
- Give a title that identifies the quantity you are seeking
in the problem or that describes the problem.
- Label the drawing, including the parameters or variables on
which the solution depends and that are given in the problem. Write
down the given values of these parameters on the drawing.
- Label any unknown parameters that must be calculated along
the way or obtained from the text in order to find the desired
solution.
- Always give the units of measure for all quantities in the
problem. If the drawing is a graph, be sure to give both the units
and the scale of the axes.
- Include on the drawing information that is assumed and not
given in the problem (such as g, the value of the acceleration due
to gravity), and whether air resistance and friction are neglected.
- Give a title that identifies the quantity you are seeking
in the problem or that describes the problem.
- Establish which general principle relates the given parameters
to the quantity that you are seeking. Usually your picture will suggest
the correct techniques and formulas. At times it may be necessary to
obtain further information from your textbook or notes before the proper
formulas can be chosen. It often happens that further information is
needed when the problem has a solution that must be calculated
indirectly from the given information. If further information is needed
or if intermediate quantities must be computed, it is here that they are
often identified.
- Draw a second picture that identifies the coordinate system and
origin that will be used in relating the data to the equations. In some
situations this second picture may be a graph, free body diagram, or
vector diagram rather than a picture of a physical situation.
- Even an expert will often use the concrete method of working a
problem. In this method you do the calculation using the given values
from the start, so that the algebra gives numerical values at each
intermediate step on the way to the final solution. The disadvantage
of this method is that because of the large number of numerical
calculations involved, mistakes are likely, and so you should take
special care with significant figures. However this method has the advantage
that you can see, at every step of the way, how the problem is
progressing. It also is more direct and often makes it easier to locate
a mistake if you do make one.
- As an expert, you will more and more use the formal method of
working a problem. In this method, you calculate the solution by doing
as much as possible without using specific numbers. In other words, do
as much of the algebra as you can before substituting the specific given
values of the data. In long and complicated problems terms may cancel or
expressions simplify. Our advice: gain experience in problem solving by
substituting the numbers when you start physics, but gradually adopt the
formal approach as you become more confident; many people adopt a
compromise approach where they substitute some values but retain others
as symbols (for example, "g" for the acceleration due to
gravity).
- Criticize your solution: Ask yourself, "Does it make
sense?" Compare your solution to any available examples or to
previous problems you have done. Often you can check yourself by doing
an approximate calculation. Many times a calculation error will result
in an answer that is obviously wrong. Be sure to check the units
of your solution to see that they are appropriate. This examination will
develop your physical intuition about the correctness of solutions, and
this intuition will be very valuable for later problems and on exams.
An important thing to remember in working physics problems is that by showing all of your work you can much more easily locate and correct mistakes. You will also find it easier to read the problems when you prepare for exams if you show all your work.
- In an examination, you may have to do problems under a strict time limitation. Therefore, when you are finished with a homework problem, practice doing it again faster, in order to build up your speed and your confidence.
It takes more time to write careful and complete solutions to homework problems. Writing down what you are doing and thinking slows you down, but more important it makes you behave more like an expert. You will be well paid back by the assurance that you are not overlooking essential information. These careful write-ups will provide excellent review material for exam preparation.
Examples of the Application of the Problem-Solving Principles
SAMPLE PROBLEM #1:
This problem is stated and the solution written down as you would work it out for homework.
In 1947 Bob Feller, former Cleveland pitcher, threw a baseball across the plate at 98.6 mph or 44.1 m/s. For many years this was the fastest pitch ever measured. If Bob had thrown the pitch straight up, how high would it have gone?
- What does the problem ask for, and what is given? Answer: The speed of
the baseball is given, and what is wanted is the height that the ball
would reach if it were thrown straight up with the given initial speed.
You should double check that whoever wrote the problem correctly
calculated that 98.6 miles/hr is equal to 44.1 m/s. You should state
explicitly, in words, that you will use the 44.1 m/s figure and that you
will assume the baseball is thrown from an initial height of zero
(ground level). You should also state explicitly what value of g you
will use, for example, g = 9.81 m/s2. You should also state
that you assume that air resistance can be neglected. Since you don't
know the mass of the baseball, say that you don't (you won't need it,
anyway).
- Make a drawing:
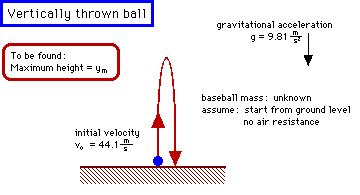
- The general principles to be applied here are those of uniformly
accelerated motion. In this case, the initial velocity vo
decreases linearly in time because of the gravitational acceleration.
The maximum height ym occurs at the time tm when
the velocity reaches zero. The average velocity during from t = 0 to t =
tm is the average of the initial velocity v = vo
and the final velocity v = 0, or half the initial velocity.
- Make a second drawing. In this case, try a graph of velocity as a
function of time:
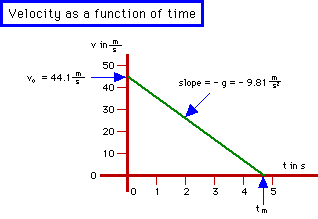
Notice that the graph is fairly accurate: You can approximate the value of g as 10 m/s2, so that the velocity decreases to zero in about 4.5 s. Therefore, even before you use your calculator, you have a good idea of about the value of tm.
- The concrete method can now be applied: An initial velocity of 44.1
m/s will decrease at the rate of 9.81 m/s2 to zero in a time
tm given by
tm = 44.1 / 9.81 = 4.4954 s .
During that time, the average velocity is vav = 44.1 / 2 = 22.05 m/s. Therefore the height is given by
ym = vav tm = 99.12 = 99.1 m .
Notice that for all "internal" calculations, more than the correct number of significant figures were kept; only when the final answer was obtained was it put into the correct number of significant figures, in this case three.
- To do this problem in a formal method, use the formula for distance y
as a function of t if the acceleration a is constant. Do not substitute
numbers, but work only with symbols until the very end:
y = yo + vo t + a t2 / 2 ,
where yo = 0 is the initial position, vo = 44.1 m/s is the initial velocity, and a = - g = - 9.81 m/s2 is the constant acceleration. However, do not use the numerical figures at this point in the calculation. The maximum value of y is when its derivative is zero; the time tm of zero derivative is given by:
dy/dt = vo + a tm = 0 --> tm = - vo / a .
The maximum height ym is given by putting this value of tm into the equation for y:
ym = yo + vo ( - vo / a ) + a ( - vo / a )2 / 2 = yo - vo2 / 2a .
Now substitute: yo = 0, vo = 44.1, a = - 9.81. The result is
ym = 0 + 0.5 (44.1)2 / 9.81 = 99.1 m/s .
- Look over this problem and ask yourself if the answer makes sense.
After all, throwing a ball almost 100 m in the air is basically
impossible in practice, but Bob Feller did have a very fast fast ball
pitch!
There is another matter: If this same problem had been given in a chapter dealing with conservation of energy, you should not solve it as outlined above. Instead, you should calculate what the initial and final kinetic energy KE and potential energy PE are in order to find the total energy. Here, the initial PE is zero, and the initial KE is m vo2 / 2. The final PE is m g ym and the final KE is zero. Equate the initial KE to the final PE to see that the unknown mass m cancels from both sides of the equation. You can then solve for ym, and of course you will get the same answer as before but in a more sophisticated manner.
- To prepare for an exam, look over this problem and ask yourself how you can solve it as quickly as possible. You may be more comfortable with the concrete approach or with the formal approach; practice will tell. On an actual exam, you might not have time for a complete drawing or a complete listing of principles. By working this problem a couple of times, even after you've gotten the answer once, you will become very familiar with it. Even better, explain the problem to a friend of yours, and that way you really will be an expert!
SAMPLE PROBLEM #2:
Again, this problem is stated and the solution written down as you would work it out for homework. As in Sample Problem #1, we go through the eight steps of the general outline.
A one kilogram block rests on a plane inclined at 27o to the horizontal. The coefficient of friction between the block and the plane is 0.19. Find the acceleration of the block down the plane.
- The problem asks for the acceleration, not the position of the block
nor how long it takes to go down the plane nor anything else. No mention
is made of the difference between static or kinetic coefficients of
friction, so assume they are the same. The mass is given, but you will
eventually find that it doesn't matter what the mass is. (If the mass
had not been given, that would be an indication that it doesn't matter,
but even in that case you may find it easier to assume a value for the
mass in order to guide your thoughts as you do the problem.)
- Here is the first picture. Note that the angle is labeled
, and the coefficient of friction is labeled 
. In addition, the use of m for the
mass and a|| for the acceleration down the plane are
defined in the picture.
- There are two general principles that apply here. The first is
Newton's Second Law:
F = m a ,
where F is the net force, a vector, and a is acceleration, another vector; the two vectors are in the same direction. The mass m will eventually be found not to make any difference, and in that case, you might be tempted to write this law as a = F / m, since a is what you want to find. However, the easiest way to remember Newton's Second Law is F = m a, and so that is the law to work with.
The second principle is that the frictional force is proportional to the normal force (the component of the force on the block due to the plane that is perpendicular to the plane). The frictional force is along the plane and always opposes the motion. Since the block is initially at rest but will accelerate down the plane, the frictional force will be up along the plane. The coefficient of friction, which is used in this proportionality relation, is
.
- It is now time to draw the second picture. It helps to redraw the
first picture and add information to it. In this case a vector diagram
is drawn and various forces are defined.
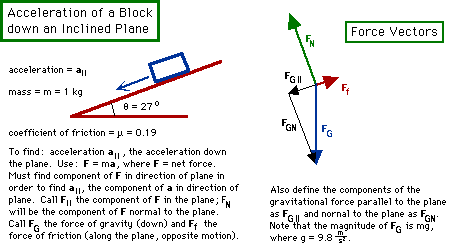
Note that in the vector diagram, the block has been replaced by a dot at the center of the vectors. The relevant forces are drawn in (all except the net force). Even the value assumed for the gravitational acceleration has been included. Some effort has been made to draw them to scale: The normal force is drawn equal in magnitude and opposite in direction to the component of the gravity force that is perpendicular to the plane. Also, the friction force has been drawn in parallel to the plane and opposing the motion; it has been drawn in smaller than the normal force. The angles of the normal and parallel forces have been carefully drawn in relation to the inclined plane. This sub-drawing has a title and labels, as all drawings should.
- We will do this problem using the formal approach, leaving the
concrete method for a check (see below).
- Now for calculation using the formal approach, where you work with
algebra and symbols rather than with numbers. First state in words what
you are doing, and then write down the equation:
- Magnitude of gravity force = weight = m g.
- Resolve gravity force into normal component and parallel component
whose magnitudes are:
FG|| = m g sin
and FGN = m g cos .
- The magnitude of the normal force due to the plane is equal in
magnitude (but the direction is opposite) to the magnitude of the
normal component of the gravity force:
FN = m g cos
.
- The frictional force opposes the motion, and its magnitude is
equal to the coefficient of friction times the normal plane force:
Ff =
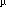m g cos .
- The net force (which is along the plane) is the difference between
the parallel component of the gravitational force and the friction
force; its magnitude is:
F = m g sin
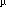- m g cos .
- The acceleration is net force over mass:
a|| = g sin
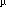- g
cos = g ( sin -
cos ) .
- The numerical answer is (given to two significant figures since
the given numbers have two):
a = (9.8 m/s2) (sin 27o - 0.19 cos 27o) = (9.8) (0.454 - 0.19 x 0.891) = 2.79 = 2.8 m/s2 .
- Magnitude of gravity force = weight = m g.
- When you look over this answer to see if it makes sense, try doing the
problem by substituting numbers in at each step (the concrete approach).
The weight of a kilogram, for example is 9.8 N. The normal
(perpendicular to the plane) component of the gravitational force is 9.8
times cos 27o or 8.73 N. This makes sense, for if the angle
were very small, the normal component of the gravitational force would
be almost equal to 9.8 itself. Notice that although the final answer
should be given to two significant figures, you should keep three in
these intermediate calculations.
The parallel component of the gravitational force is 9.8 sin 27o = 4.45 N. The normal force due to the plane is equal in magnitude to the gravitational normal force (but opposite in direction), and so the frictional force is 0.19 times 8.73 or 1.66 N. The net force is down the plane and equal to the difference 4.45 - 1.66 = 2.79 N. Divide this value by 1 kg to get the acceleration 2.79 m/s2 (which is rounded off to 2.8f m/s2).
Again examine your solution. It says that the block does accelerate down the plane because the final answer is positive. The acceleration is less than g, again a reasonable result. Notice that if the angle were more than 27o, then its sine would be larger and its cosine smaller, so the acceleration would be greater. If the angle were less than 27o then the opposite would be true, and the acceleration, as calculated above, could become negative. But a negative value for acceleration would be wrong, because that would say that the block would accelerate up the plane because the frictional force dominates, and that is impossible. Instead, if the calculation had produced a negative value for a, you would have had to change the solution to a = 0, meaning that the frictional force was enough to prevent sliding.
- Now anticipate how you'd do this problem on an exam. Is the concrete approach faster and easier for you? Or would you be more comfortable using the formal approach on an exam? It is a good idea to practice doing this problem when you study for an exam, if you think a similar problem will be asked.
Effective Test Preparation
If you have followed an active approach to study similar to the one suggested in this handout, your preparation for exams will not be overly difficult. If you haven't been very active in studying, your preparation will be somewhat harder, but the same principles still apply. Always remember: Physics courses, and therefore physics exams, involve problem solving. Hence, your approach to studying for exams should stress problem solving.Here are some principles:
- In the week prior to the exam, follow the three steps below.
These steps should give you a reasonably good idea of what has been
stressed and on what you can expect to be tested.
- Review your notes and recheck the course outline. Your goal
at this point is to make sure you know what has been emphasized.
- Reread your solutions to the homework problems. Remember
that these solutions, if complete, will note underlying principles
or laws.
- Review the assigned chapters. Once again, your purpose in
this early stage of exam preparation is to make sure you know what
topics or principles have been emphasized.
- Review your notes and recheck the course outline. Your goal
at this point is to make sure you know what has been emphasized.
- From this rapid overview, generate a list of themes, principles,
and types of problems that you expect to be covered. If samples
of previous exams are available, look them over, also, but do not assume
that only previous types of problems will be included. It definitely
helps to work with others at this stage.
- Review actively. Don't be satisfied with simple recognition of
a principle. Aim for actual knowledge that you will be able to recall
and to use in a test situation. Try to look at all the possible ways
that a principle can be applied. Again, it helps to work with others and
to explain things to others (and have them explain things to you).
For example: If velocity and acceleration principles have been emphasized in the course, look over all of your homework problems to see if they illustrate these principles, even partially. Then if you also can anticipate an emphasis on friction and inertia, once again review all of your homework problems to see if they illustrate those principles.
- Effective examination preparation involves an interaction among
homework problems, the classes, your notes and the text. Review
actively, including self-tests in which you create your own problems
which involve a combination of principles. You need to be sure that you
can work problems without referring to your notes or to the textbook.
Practice doing problems using both the concrete and the formal
approaches, to see which you are more comfortable with.
- Remember that exams will include a variety of different
problems. You want to look back on an exam and say, "I know how to
do friction problems so well, that even though they were asked in a
weird way, I could recognize them and solve them."
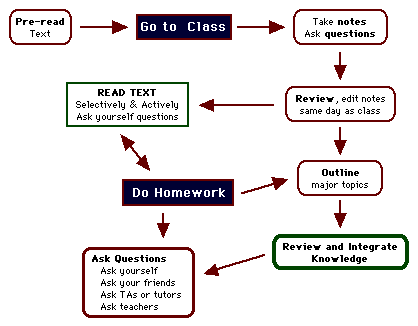
Weekly Flow Chart for Studying Physics
Tips
These tips are based on a list "17 Tips that UT Seniors Wish They'd Known as Freshmen" by Dr. John Trimble, a professor in the English Department. He is a member of The University of Texas's Academy of Distinguished Professors. These tips have been adapted to fit physics courses, but they are good tips for any university student. I have abbreviated most of these tips but have not omitted any. You can find the complete version at the Learning Skills Center (and elsewhere).
- Get to know your professor. Go to his or her office hours early in the
semester and often. Go to their office hours early in the semester and
often.
- As soon as you can, trade names and phone numbers with at least two
classmates. Don't ask the professor what you missed if you happen to
miss class; ask your classmates.
- Make sure you are enrolled in the course you think you are enrolled
in. Correct any enrollment mistakes as soon as you can.
- Read and study your course policy statement (the first day handout or
the syllabus). It is a legal contract!
- Buy and use an appointment book.
- Keep a notebook of unfamiliar words and phrases. Look them up or ask
what they mean. Buy and use a good dictionary.
- If you haven't yet learned to use a computer, do so. If you don't have
a good calculator, which you know how to use easily, buy one and learn
to use it. A particular calculator may be required for class; be sure
you get the right one. Study its manual and practice using it until you
can do so quickly and accurately.
- Learn to touch-type. If you hunt-and-peck, you will be at a
disadvantage. Learn either through a computer program such as Maevis
Beacon.
- Bring two calculators to each exam or one calculator and extra
batteries. Bring your text book to each exam. Bring extra paper to each
exam. Bring two pencils and two pens to each exam. Bring two blue books
if required. Ask which of these you are allowed to use, but of course
don't use the items that aren't allowed.
- Go to each and every class session. Be punctual. Look professional.
Don't disturb the class by talking. But do ask questions!
- Exercise at least every other day.
- When you write papers, do so in at least two editing stages, with a
few hours or a day or two between drafts. Type your papers. When you
write up homework problems, do so neatly and carefully. If possible, ask
your instructor, or the grader for feedback before you turn in the final
version of an assignment.
- Understand that you are reinventing yourself. You are defining what
and who you are for a good many years to come (you may want to reinvent
yourself later, at 30 or 40), so be careful about how you go about it.
- Hang out with the smartest, most studious people you can find. Watch
how they work. Eventually people will be watching you; help them in
developing good study habits.
- Take the teacher, not the course. Shop for the best teachers by asking
older students who they are. Try to meet prospective teachers before
enrollment. Keep a "Best Teachers/Best Courses" notebook.
- Assume responsibility for your own education. Exercise initiative.
Learn to love the whole process of education, not just the end-product.
- Dr. Trimble's seven reasons for going to college:
- To meet a lot of interesting people, some of whom will become
lifelong friends.
- To gain an enlarged view of an enlarged world.
- To learn better how to learn. (Most of what you later learn,
you'll teach yourself.)
- To reinvent yourself -- that is, to discover and explore more of
yourself than you normally could at home.
- To acquire at least a dilettante's knowledge about a lot of
different things, since being informed beats the hell out of being
ignorant.
- To learn how to handle adult responsibilities while still enjoying
a semi-protected environment.
- To identify and explore career options.
- To meet a lot of interesting people, some of whom will become
lifelong friends.