Strong-randomness infinite-coupling phase in a random quantum spin chain

We study the ground-state phase diagram of the Ashkin-Teller random quantum spin chain by means of a generalization of the strong-disorder renormalization group. In addition to the conventional paramagnetic and ferromagnetic (Baxter) phases, we find a partially ordered phase characterized by strong randomness and infinite coupling between the colors. This unusual phase acts, at the same time, as a Griffiths phase for two distinct quantum phase transitions both of which are of infinite-randomness type. We also investigate the quantum multi-critical point that separates the two-phase and three-phase regions; and we discuss generalizations of our results to higher dimensions and other systems.

Fawaz Hrahsheh, Rajesh Narayanan, José A. Hoyos, Thomas Vojta (Manuscript)

arXiv:1310.4864

Disordered bosons in one dimension: from weak to strong randomness criticality

We investigate the superfluid-insulator quantum phase transition of one-dimensional bosons with off-diagonal disorder by means of large-scale Monte-Carlo simulations. For weak disorder, we find the transition to be in the same universality class as the superfluid-Mott insulator transition of the clean system. The nature of the transition changes for stronger disorder. Beyond a critical disorder strength, we find nonuniversal, disorder-dependent critical behavior. We compare our results to recent perturbative and strong-disorder renormalization group predictions. We also discuss experimental implications as well as extensions of our results to other systems.

Fawaz Hrahsheh, Thomas Vojta, Phys. Rev. Lett. 109, 265303 (2012)

arXiv:1210.4807

Rounding of a first-order quantum phase transition to a strong-coupling critical point

We investigate the effects of quenched disorder on first-order quantum phase transitions on the example of the N-color quantum Ashkin-Teller model. By means of a strong-disorder renormalization group, we demonstrate that quenched disorder rounds the first-order quantum phase transition to a continuous one for both weak and strong coupling between the colors. In the strong coupling case, we find a distinct type of infinite-randomness critical point characterized by additional internal degrees of freedom. We investigate its critical properties in detail and find stronger thermodynamic singularities than in the random transverse field Ising chain. We also discuss the implications for higher spatial dimensions as well as unusual aspects of our renormalization-group scheme.

Fawaz Hrahsheh, José A. Hoyos, Thomas Vojta, Phys. Rev. B 86, 214204 (2012)

arXiv:1208.0471

Infinite-randomness criticality in a randomly layered Heisenberg magnet

We study the ferromagnetic phase transition in a randomly layered Heisenberg magnet using large-scale Monte-Carlo simulations. Our results provide numerical evidence for the infinite-randomness scenario recently predicted within a {strong-disorder renormalization group approach}. Specifically, we investigate the finite-size scaling behavior of the magnetic susceptibility which is characterized by a non-universal power-law divergence in the Griffiths phase. We also study the perpendicular and parallel spin-wave stiffnesses in the Griffiths phase. In agreement with the theoretical predictions, the parallel stiffness is nonzero for all temperatures T < T_c. In contrast, the perpendicular stiffness remains zero in part of the ordered phase, giving rise to anomalous elasticity. In addition, we calculate the in-plane correlation length which diverges already inside the disordered phase at a temperature significantly higher than T_c. The time autocorrelation function within model A dynamics displays an ultraslow logarithmic decay at criticality and a nonuniversal power-law in the Griffiths phase.

Fawaz Hrahsheh, Hatem Barghathi, Thomas Vojta, Phys. Rev. B 84, 184202 (2011)

arXiv:1109.4172

Composition-tuned smeared phase transitions

Phase transitions in random systems are smeared if individual spatial regions can order independently of the bulk system. In this paper, we study such smeared phase transitions (both classical and quantum) in substitutional alloys A_(1-x)B_x that can be tuned from an ordered phase at composition x=0 to a disordered phase at x = 1. We show that the ordered phase develops a pronounced tail that extends over all compositions x < 1. Using optimal fluctuation theory, we derive the composition dependence of the order parameter and other quantities in the tail of the smeared phase transition. We also compare our results to computer simulations of a toy model, and we discuss experiments.

Fawaz Hrahsheh, David Nozadze, and Thomas Vojta, Phys. Rev. B 83, 224402 (2011)

arXiv:1103.5439

Disorder correlations at smeared phase transitions

We investigate the influence of spatial disorder correlations on smeared phase transitions, taking the magnetic quantum phase transition in an itinerant magnet as an example. We find that even short-range correlations can have a dramatic effect and qualitatively change the behavior of observable quantities compared to the uncorrelated case. This is in marked contrast to conventional critical points, at which short-range correlated disorder and uncorrelated disorder lead to the same critical behavior. We develop an optimal fluctuation theory of the quantum phase transition in the presence of correlated disorder, and we illustrate the results by computer simulations. As an experimental application, we discuss the ferromagnetic quantum phase transition in Sr_1-xCa_xRuO₃.

Christopher Svoboda, David Nozadze, Fawaz Hrahsheh, Thomas Vojta, Europhys Lett. 97, 20007 (2012)

arXiv:1109.4290

Disorder promotes ferromagnetism: Rounding of the quantum phase transition in
Sr_1-xCa_xRuO₃

The subtle interplay of randomness and quantum fluctuations at low temperatures gives rise to a plethora of unconventional phenomena in systems ranging from quantum magnets and correlated electron materials to ultracold atomic gases. Particularly strong disorder effects have been predicted to occur at zero-temperature quantum phase transitions. Here, we demonstrate that the composition-driven ferromagnetic-to-paramagnetic quantum phase transition in Sr_1-xCa_xRuO₃ is completely destroyed by the disorder introduced via the different ionic radii of the randomly distributed Sr and Ca ions. Using a magneto-optical technique, we map the magnetic phase diagram in the composition-temperature space. We find that the ferromagnetic phase is significantly extended by the disorder and develops a pronounced tail over a broad range of the composition x. These findings are explained by a microscopic model of smeared quantum phase transitions in itinerant magnets. Moreover, our theoretical study implies that correlated disorder is even more powerful in promoting ferromagnetism than random disorder.

L. Demko, S. Bordacs, T. Vojta, D. Nozadze, F. Hrahsheh, C. Svoboda, B. Dora, H. Yamada, M. Kawasaki, Y. Tokura, I. Kezsmarki, Phys. Rev. Lett. 108, 185701 (2012)

arXiv:1202.3810

Nucleation Rates of Methanol Using the SAFT-0 Equation of State

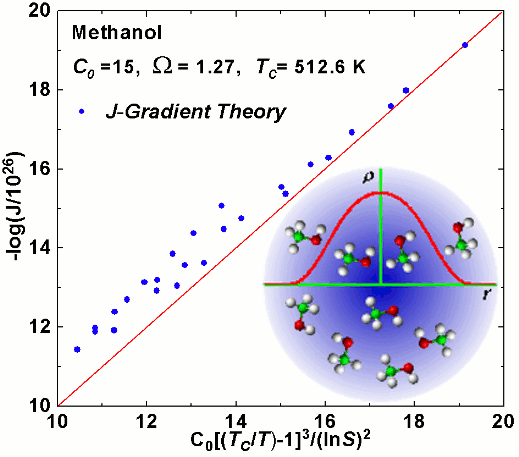
Classical and nonclassical calculations of nucleation rates are presented for methanol, an associating vapor system. The calculations use an equation of state (EOS) that accounts for the effects of molecular association based on the statistical association fluid theory (SAFT). Two forms of classical nucleation theory (CNT) were studied: a Gibbsian form known as the P-form and the standard or S-form. CNT P-form calculations and nonclassical gradient theory (GT) calculations were made using the SAFT-0 EOS. Calculated rates were compared to the experimental rates of Strey, et al. [J. Chem. Phys.1986, 84, 2325–2335]. Very little difference was found between the two forms of CNT for either the temperature (T) or supersaturation (S) dependence of the rates. Nucleation rates based on GT showed improved T and S dependence compared to CNT. The GT rates were also improved by factors of 100-1000 compared to CNT. Despite these improvements, GT does not describe the reported T and S dependence of the nucleation rates. To explore this further, the GT and experimental rates were analyzed using Hale’s scaled model [J. Chem. Phys.2005, 122, 204?509]. This analysis reveals an inconsistency between the predictions of GT, which scale relatively well, and the experimental data, which do not scale. It also shows that the measured rate data have an anomalous T and S dependence. A likely source of this anomaly is the inadequate thermodynamic data base for small cluster properties that was used originally to correct the raw rate data for the effects of association.

Abdalla Obeidat, Maen Gharaibeh, Hasan Ghanem, Fawaz Hrahsheh, Nora Al-Zoubi, and Gerald Wilemski, ChemPhysChem 2010, 11, 3987–3995.

Direct Link to pdf copy