CHAPTER FIVE

Sampling Distributions

In this chapter we will introduce one of the most important concepts in statistics, that of the sampling distribution.

Example 5.1: A population consisting of exam grades of N = 5 students taking the Engineering Statistics course is described below

Table 1 Distribution of Grades for the Engineering Statistics Class

Name

Ordinal Grade

Grade Points

Mohammad

Abdallah

Khaled

Ali

Saad

It is easy to check that for grade points (), the mean and variance are given by

Now consider a sample of size 2, and prepare all possible samples without replacement. In fact, there will be samples without replacement. The sample means and the corresponding probabilities are tabulated below:

Table 2 All Possible Samples of Size 2 with their Probabilities

	Sample Units	P(=)
2.0	(Abdallah, Saad)	0.10
2.5	(Mohammad, Abdallah), (Mohammad, Saad) (Abdallah, Khaled), (Khaled, Saad)	0.40
3.0	(Mohammad, Khaled), (Abdallah, Ali), (Ali, Saad)	0.30
3.5	(Mohammad, Ali), (Khaled, Ali)	0.20

The expected value of the sample mean is

which is the same as the population mean . The expected value of is given by

so that .

It may be shown that

That is the variance of the sample mean can be calculated from the population variance . Note that in case of sampling with replacement with large , we have and consequently, .

5.1 Sampling Distributions of Sums and Means and the Central Limit Theorem

Example 5.2 One hundred bolts are packed in a plastic box. The weight of the empty box can be ignored. However, each bolt weighs around 1 ounce with standard deviation s = 0.01 ounce. Assume that weights of bolts follow a normal distribution.

(a) Find the probability that a box filled with hundred bolts weighs more than 100.196 ounces.

(b) Find the probability that the mean weight of 100 bolts is more than 1.00196 ounces.

Solution

(a)

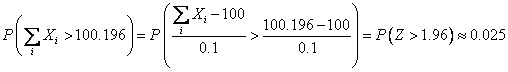(b) Since

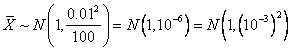Note that the events in (a) and (b) are equivalent.

Example 5.3 The weights of ball bearings have a distribution with a mean of 22.40 ounces and a standard deviation of 0.048 ounces. If a random sample of size 36 is drawn from this population, find the probability that the sample mean lies between 22.39 and 22.42.

Solution Let X = weight of a ball bearing. Then

and

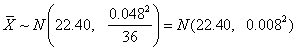
and hence

5.2 The Normal Approximation to the Binomial Distribution

Let X be a binomial random variable with trials and success probability p. Then probabilities of events related to X can be approximated by a normal distribution with mean and variance if the conditions and are satisfied.

Continuity Correction

It is the adjustment made to an integer-valued discrete random variable when it is approximated by a continuous random variable. For a binomial random variable, we inflate the events by adding or subtracting 0.5 to the event as follows:

The continuity correction should be applied anytime a discrete random variable is being approximated by a continuous random variable.

Example 5.4 The pass mark in an examination is the median mark. A random sample of 10 candidates is chosen after the examination.

(a) What is the distribution of the random variable “the number of students who passed the examination”?

(b) Find the probability that more than 2 of the selected candidates passed the examination.

(d) Solve parts (b) and (c) using the normal approximation.

Solution

(a) Any candidate picked either passes or fails the examination (i.e. mutually exclusive outcomes at each trial). Since the pass mark is the median mark, it means that 50% of the candidates passed the examination so that The trials are assumed to be independent. Thus, the random variable “the number of students who passed the examination” is a binomial random variable with n = 10 and p = 0.5.

(b) If we represent the random variable in (a) by X, then we are interested in the probability . By the use of binomial probability we have

whereas by using Statistica we have:

(d) Since, we use the normal approximation to binomial and so the random variable X has a normal distribution with mean and variance So to solve the problems based on the approximation, open the Normal Probability Calculator, put 5 for the mean and for the standard deviation.

For the problem in part (b), we have

For the problem in part (c), we have

5.3 Drawing a Random Sample from a known Distribution

Random samples are drawn from a known distribution by evaluating the inverse cumulative distribution functions at random probabilities. For example, suppose a random variable has a cumulative distribution function F, i,e, , where x is a value in the domain of X, and hence . Thus by supplying random values between 0 and 1 for p, we obtain values of x, which constitute a random sample from the distribution with cumulative distribution function F.

The V-functions and Rnd function

In Statistica, the V-functions are the inverse cumulative distribution functions and can be found in the Function Wizard. There is VNormal for the normal distribution, VExpon for the exponential distribution, and so on.

Another function in the Function Wizard is the Rnd(x) function, which gives random numbers between 0 and x. For example, Rnd(1) gives a random number between 0 and 1, which can be used to represent random probability values.

Sampling from the Normal Distribution

The inverse cumulative distribution function of the normal distribution is where x is a probability value, mu is the mean of the normal distribution and sigma is its standard deviation. To draw a random sample from the normal distribution with mean 60 and variance 25, we summarize the steps below:

1. Double-click VAR1

2. Type =Rnd(1) in the formula box

3. OK/Yes

4. Double-click VAR2

5. Type the equal sign “=” in the formula box

6. Functions/Distributions, Double-click VNormal

7. x = v1, mu = 60 and sigma = 5

8. OK/Yes.

The values given in VAR2 constitute the required sample. Alternatively, we can obtain the sample without using two columns of our data sheet. For example, if we wish to have our sample in VAR3, we will proceed as follows:

1. Double-click VAR3

2. Type the equal sign “=” in the formula box

3. Functions/Distribution, Double-click VNormal

4. x = Rnd(1), mu = 60 and sigma = 5

5. OK/Yes.

Sampling from the Exponential Distribution

The inverse cumulative distribution function of the exponential distribution is VExpon(x, lambda), where x is a probability value and lambda is the parameter of the exponential distribution. Care must be taken when supplying the value for lambda. For example, if we are sampling from an exponential distribution with parameter k, we directly substitute k for lambda. On the other hand, if we are sampling from an exponential distribution with mean k, we substitute 1/k for lambda. To draw a sample from the exponential with parameter 0.5, follow the steps:

1. Double-click VAR1

2. Type = Rnd(1) in the formula box

3. OK/Yes

4. Double-click VAR2

5. Type the equal sign “=” in the formula box

6. Functions/Distributions, Double-click VExpon

7. x = v1, lambda = 0.5

8. OK/Yes.

Here, we can also draw the random sample using only one column of our data sheet as follows:

1. Double-click VAR3

2. Type the equal sign “=” in the formula box

3. Functions/Distributions, Double-click VExopn

4. x = Rnd(1), lambda = 0.5

5. OK/Yes.

100 random samples each of size 30 are drawn from the exponential distribution with mean ; their means are tabulated below:

Table 3 Means of 100 Random Samples of Size 30 from the ExponentialDistribution

Sample		Sample		Sample		Sample
1	2.184054	26	2.082070	51	2.282192	76	1.783575
2	1.814839	27	1.445744	52	1.504987	77	1.587805
3	1.845744	28	1.758239	53	2.398457	78	2.620010
4	2.204828	29	1.997465	54	2.227194	79	1.679762
5	2.556562	30	1.758824	55	2.314496	80	1.274267
6	1.931955	31	1.850869	56	1.866983	81	2.160579
7	2.179001	32	1.393448	57	1.697291	82	1.310457
8	1.977819	33	1.849390	58	1.483425	83	2.149534
9	2.580562	34	1.806390	59	2.121959	84	2.210060
10	2.116091	35	2.342794	60	2.005428	85	2.403257
11	1.992988	36	1.872477	61	2.249343	86	1.801674
12	2.321373	37	1.948877	62	1.733591	87	1.759119
13	2.037973	38	1.829172	63	1.718578	88	2.018302
14	2.437841	39	1.457925	64	1.296010	89	1.549417
15	2.149032	40	2.142974	65	2.332216	90	2.446048
16	1.758222	41	2.096374	66	1.944724	91	1.754672
17	1.756615	42	1.900634	67	2.360446	92	1.968279
18	2.027894	43	2.054499	68	2.815900	93	1.729697
19	2.010520	44	2.077696	69	2.436328	94	1.959883
20	1.877407	45	2.126649	70	2.168109	95	2.062244
21	1.711968	46	2.091533	71	1.683284	96	1.808607
22	1.823209	47	2.304099	72	2.290407	97	1.378574
23	2.750169	48	1.565620	73	1.601436	98	1.950490
24	2.146609	49	2.700095	74	1.694431	99	1.888556
25	1.933193	50	2.321632	75	2.279583	100	2.009424

One hundred means given in Table 3 have been used to draw a histogram (See Figure 5.1) which is approximately bell shaped. The larger the sample sizes, the better would be the approximation towards normal frequency curve.

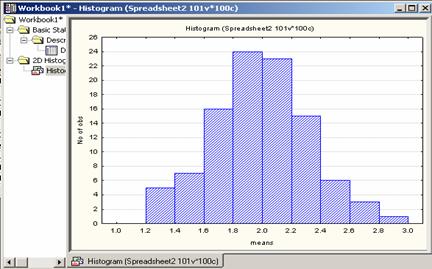
Figure 5.1 Histogram of the sample in Table 3

5.4 Use of t , and F Tables

Using the student t table in Appendix A3 we can find the following:

For a t random variable with 8 degrees of freedom, P(t > 2.896) = 0.01

For a t random variable with 17 degrees of freedom, P (t < –2.898) = 0.005

For a t random variable with 21 degrees of freedom, P (t < –1.721) = 0.05

Using the table in Appendix A4 we can find the following:

For a random variable with 7 degrees of freedom, P(> 2.17) = 0.95

For a random variable with 17 degrees of freedom, P(< 33.41) = 0.99

For a random variable with 28 degrees of freedom, P(> 48.28) = 0.01

Using the F table in Appendix A5 we can find the following:

For an F random variable with 4 and 7 degrees of freedom, P(F > 4.12) = 0.05

For an F random variable with 15 and 21 degrees of freedom, P(F > 2.534) = 0.025

For an F random variable with 12 and 9 degrees of freedom, P(F > 5.111) = 0.01

5.5 The Probability Calculator for t, and F Distributions

The t Probability Calculator

In the Probability Distribution Calculator, select t (Student) for the -distribution (see Figure 5.2) and supply the Degrees of Freedom (df).

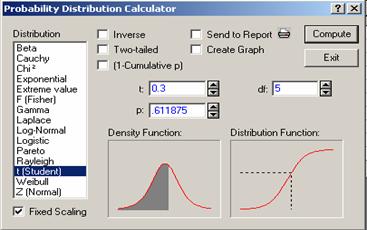
Figure 5.2 Probability Calculator for the t-distribution

It is important to note that the t random variable is symmetric about zero regardless of the value of the df.

Figure 5.2 shows that for the t random variable with 5 df, the probability that t is less than 0.3 is 0.611875, i.e., , where has a Student t-distribution with 5 degrees of freedom. The Two-tailed and (1-Cumulative p) probabilities and their combinations are computed in the same way as done for standard normal random variable.

The value is the value of t random variable for a given df that has an area (or a probability) of to its right. The value is similarly defined.

The Chi-Square Probability Calculator

Selecting Chi² under Probability Distribution Calculator gives the calculator for chi-square random variable. Just as in the case of t-distribution, the parameter to be supplied here is the df. However, the Two-tailed on this calculator is disabled and cannot be used. The (1-Cumulative p) and the Inverse function are used the same way as done for the normal distribution.

The F Probability Calculator

To get the probability calculator for the F distribution, we select F from the list of distributions. Here, we are required to supply two parameters; the first and the second df (df1 and df2) respectively. Figure 5.3 shows that for F distribution with 3 and 20 df, the 95^th percentile is 3.098389.

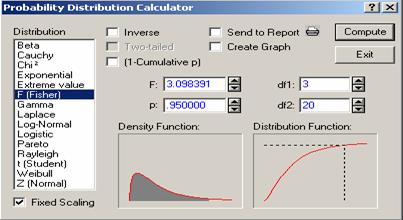
Figure 5.3 Probability Calculator for the F distribution

Note that the Two-tailed on this calculator is disabled and cannot be used.

Exercises

5.1 (Johnson, R. A., 2000, 212). A random sample of size 100 is taken from an infinite population having a mean, 76 and a variance, 256. What is the probability that the sample mean will be between 75 and 78?

5.2 (Johnson, R. A., 2000, 212). A wire- bonding process is said to be in control if the mean pull-strength is 10 pounds. It is known that the pull-strength measurements are normally distributed with a standard deviation of 1.5 pounds. Periodic random samples of size 4 are taken from this process and the process is said to be “out of control” if a sample mean is less than 7.75 pounds. Comment.

5.3 The weights of ball bearings have a distribution with a mean of 22.40 ounces and a standard deviation of 0.048 ounces. If a random sample of size 49 is drawn from this population, find the probability that the

(a) sample mean lies between 22.36 and 22.41,

(b) sample mean is more than 22.38,

(d) sample mean is greater than or equal to 22.41.

5.4 Suppose X is normally distributed with mean 50 and variance 9. Let be a random variable in the sense of drawing repeated samples of size 16 from the distribution of X. Find the probability that

(a) differs from the mean by less than 2.5 units,

(b) differs from the mean by more than 1.5 units,

5.5 Consider a binomial random variable with 50 trials and success probability 0.39.

(a) Compute the probability that it is at least equal to 15.

(b) Compute the probability that it is at most equal to 12.

(d) Compute the probability that it is equal to 30.

(e) Repeat (a) to (d) using the normal approximation to the binomial.

5.6 Consider a binomial random variable with 100 trials and success probability 0.45.

(a) Compute the probability that it is at least equal to 25.

(b) Compute the probability that it is at most equal to 32.

(d) Compute the probability that it is equal to 40.

(e) Repeat (a) to (d) using the normal approximation to the binomial.

5.7 Draw a random sample of size 200 from a normal distribution with mean 40 and variance 36. Compute the mean and standard deviation of your sample.

5.8 Draw a random sample of size 60 from a normal distribution with mean 10 and variance 4. Compute the mean and standard deviation of your sample.

5.9 Draw a random sample of size 100 from a normal distribution with mean 20 and variance 25. Compute the mean and standard deviation of your sample.

5.10 Draw a random sample of size 100 from an exponential distribution with λ = 4. Compute the mean and standard deviation of your sample.

5.11 Draw a random sample of size 120 from an exponential distribution with mean 2. Compute the mean and standard deviation of your sample.

5.12 Suppose X is normally distributed with mean 60 and variance 16. Find the probability that based on samples of size 9, differs from the mean by less than 2.5 units.

5.13 Consider a binomial random variable with 20 trials and success probability 0.45.

(a) Compute the probability that it is at least equal to 3.

(b) Compute the probability that it is at most equal to 12.

(d) Compute the probability that it is equal to 12.

(e) Repeat (a) to (d) using the normal approximation to binomial.

5.14 Draw a random sample of size 36 from a normal distribution with mean 10 and variance 4. Compute the mean and standard deviation of your sample.

5.15 Consider an exponential distribution with expected value 10. Draw samples of size from the above population. Draw a relative frequency histogram and relative frequency curve for the 100 sample means. Repeat the experiment with samples of size . What is the sampling distribution of the sample means?