
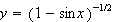 is defined on any interval
is defined on any interval






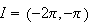 or
or

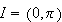 ...etc.
...etc.
24(a)

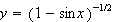 is defined on any interval
is defined on any interval

![]() such that
such that

![]() Clearly
Clearly

![]() Then
Then

![]() could be any interval on which
could be any interval on which

![]() e.g.,
e.g.,

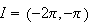 or
or

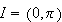 ...etc.
...etc.
For

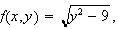

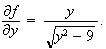 Both functions are continuous when
Both functions are continuous when

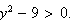 i.e.,
i.e.,

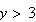 or
or

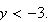 Then the domain of continuity of both functions is
Then the domain of continuity of both functions is

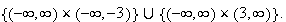
21.
Since

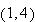 belongs to the domain of continuity , then Theorem 1.1 guarantees the existence
of a unique solution.
belongs to the domain of continuity , then Theorem 1.1 guarantees the existence
of a unique solution.
22.
Since

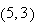 is not in the domain of continuity, Theorem 1.1 does not guarantee the
existence or the uniqueness of a solution.
is not in the domain of continuity, Theorem 1.1 does not guarantee the
existence or the uniqueness of a solution.