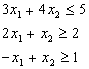
min
s. t.
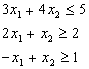
3 4 1 0 0 0 0 5
2 1 0 -1 0 1 0 2
-1 1 0 0 -1 0 1 1
0 0 0 0 0 1 1 0
3 4 1 0 0 0 0 5
2 1 0 -1 0 1 0 2
-1 1 0 0 -1 0 1 1
-1 -2 0 1 1 0 0 -3
pivot on a32
7 0 1 0 4 0 -4 1
3 0 0 -1 1 1 -1 1
-1 1 0 0 -1 0 1 1
-3 0 0 1 -1 0 2 -1
pivot on a11
1.0000 0 0.1429 0 0.5714 0 -0.5714 0.1429
0 0 -0.4286 -1.0000 -0.7143 1.0000 0.7143 0.5714
0 1.0000 0.1429 0 -0.4286 0 0.4286 1.1429
0 0 0.4286 1.0000 0.7143 0 0.2857 -0.5714
The original is not feasible
b. The first and present simplex tableau are as follows
2 c d 1 0 6
-1 3 e 0 1 1
a 1 -2 0 0 0
|
|
g 2 -1 0.5 m f h i 1 0.5 1 p n 7 j k b 9 |
Find
a to p.SOLUTION
It is clear that at every iteration there will be at least two basic vectors with
1 at the basic variable and 0's else where therefore in the present tableau
the first and fifth vectors are the basic vectors. Now since 1 is in 5th vector
then the rest is zero i.e.
m=b=0.
Also the first vector is basic this implies
g=1,h=n=0.
Using the simplex method in matrix form i.e.
=
Now 
then using the above six equality you will find that
a=-3,k=1.5,c=4,j=-5i=5,e=0,d=-2,f=3,p=4.
