a) What could be the maximum rank of A?
The maximum rank could not exceed the number of unknowns.
So, the maximum rank is 3.
b) If the rank of A is equal to the number of unknowns,
find the solution of the system. Write your answer
in vector form.
The only solution of the system will be the trivial
solution. Thus,
c) If the rank of A is 1, how many free variables will
be involved in the solution? Justify your answer.
number of free variables = 3 - 1 = 2
7. Let ei
be the 2 x 1 i-th basic unit vector and let A be
a 2 x 2 matrix such that
Use Cramer's rule to solve the linear system
Using the property that Aei
= the i-th column of A, we have
(reinitialize the vector x)
The only other method we know to compute the inverse
of a matrix is to compute the reduced echelon form
of the augmented matrix of of [ B | I ]
(define I as the 3 x 3 identity matrix)
(form the augmented matrix and name it BI)
(Compute the reduced row ech. form of BI)
(Extract the inverse from BI)
c)
Give your observation about the relationship between
the rows of A and B and the columns of A-1 and B-1
(Display the matrices in question)
We observe that B can be obtained form A by interchanging
row 1 and row 3 of A,
and B-1
can be obtained form A-1
by interchanging column 1 and column 3 of A-1.
6. Consider the homogenous linear system Ax = 0. Let
A be a 4 x 3 matrix
(property of determinant of the product)
11. Justify the following statements (give the reason
why they are true)
a) Cramer's rule can't be used for solving non-square
linear systems
Cramer's rule requires the use of determinants and determinants
are not defined for non square matrices.
b) Homogenous linear systems have at least one solution
All homogeneous systems have the trivial solution
c) The inverse matrix method can't be used to solve
the system Ax = b if | A | = 0.
If | A | = 0, then A is not invertible and the inverse
matrix method requires the use of the inverse of A.
12. Answer the following questions by (T)rue or (F)alse
Note:
An incorrect answer will cancel one correct answer.
(F) If x and y are solutions to the nonhomogeneous system
then their sum is a solution to the homogenous equation
Ax = 0.
(T)
If x and y are two solutions of the homogenous system
Ax = 0 then their sum z = x + y is also a solution
to the system.
(F) If A and B are square matrices and AB = AC, then
B = C.
(T) If A and B are invertible matrices, then

(T)
If A is invertible then the linear system Ax = 0 has
only the trivial solution.
(F) A nonzero diagonal matrix is always invertible.
(T)
If A is row equivalent to an identity matrix, then the
linear system Ax = b has a unique solution.
(T)
A nonhomogenous linear system with less equations than
unknowns always has either no solution or infinite
number of solutions.
(F)
If the intersections of three lines in a plane form
a triangle, then the linear system representing the
three lines has three solutions.
(F)
If the reduced row echelon form of the coefficient matrix
of a nonhomogeneous linear system has a leading entry
in the last column, then the system has no solution.
(F) If A is an n x n matrix then
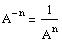
.
(F)
If a square matrix A is row equivalent to identity matrix
I, then | A | = 1.
(F) If A and B are m x n matrices then, | A + B | =
| A | + | B |.
(T) If A and B are m x n matrices then,
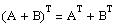
.
(F) A square matrix A is orthogonal if A-1 = A.
(F)
A linear system with less unknowns than equations is
always consistent.
(F)
If A is a square matrix with no zero rows or columns,
then A is nonsingular.
(T) If A is invertible and AB = 0 then B = 0.
(F) If k is a nonzero constant, then
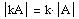
.
(T) Students should work to earn their grades and not
beg for them.
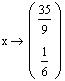
8. Show that if x and y are two solutions of the nonhomogenous
system Ax = b, then their difference z =
x - y is a solution to the homogenous system Ax = 0.
x is a solution ==> Ax = b
y is a solution ==> Ay = b
The sum x + y will be a solution to the homogenous system
Ax = 0 if we can show that A(x + y) = 0
Thus, x + y is a solution to the homogeneous system.
9. If a, b, and c are nonzero real numbers, find the
inverse of the matrix
(Augment A with the 3 x 3 Ident. matrix)
10. if A and B are 3 x 3 matrices such that (AB)
T =
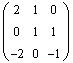
and A =
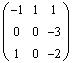
a) find
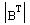
(property of transpose of the product)
Therefore, the solution is
If possible, give examples of a reduced row echelon
form of the augmented matrix of a linear system with
the given conditions. If not possible, write "Impossible"
as an answer.
Note: Use ' * ' to indicate that an element can be any
real number
a) a nonhomogeneous system with 4 equations in 3 unknowns
that has no solution
Math260-032 (A. Farhat) Solution of Major Exam
1
2. Solve the initial value problem
Therefore, the solution is
Remark:
The problem can also be solved as an exact equation
if rewritten in the form
(Compute the transpose of Ad)
(Compute the determinant of A)
(Compute the inverse of A and name it A_inv)
b) Use another method to compute the inverse of the
matrix
The matrix
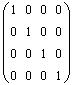
i
s not a valid answer because on one hand it says that
we can solve for the tree unknowns (they are all zeros),
and on the other hand it says that the system has no
solution (due to the leading entry in the last column)
Another way to justify that it is a wrong answer is
to compare the number of unknowns and the rank of the
matrix. Here we have
Number of unknowns = 3, Rank = 4 ( not
possible since the rank could never
exceed the number of unknowns)
Alternatively,
# of free variable = # of unknowns - rank
= 3 - 4 = -1 (not possible)
b) a nonhomogeneous system with 4 equations in 3 unknowns
that has a unique solution
c) a nonhomogeneous system with 4 equations in 3 unknowns
that has infinite number of solutions
d) a homogeneous system with 3 equations in 4 unknowns
that has only the trivial solution
Not possible because the reduced row echelon form of
the augmented matrix of a homogeneous system with 3
equations has a maximum rank equal to 3. And since
# of free variables
= # of unknowns - rank
there will be at least one free variable.
5 a) Use the adjoint method to compute the inverse of
the matrix
(Set the starting subscript for Mathcad to 1)
Compute the cofactors as elements of a matrix named
Ad