e) Supply the arguments to the rkfixed command. The
returned values will be stored in a matrix we
will call S.
The matrix S will have 5 columns. Describe the values
represented by each column.
first column =
2nd column =
3rd column =
4th column =
5th column =
f) The given IVP was solved in part (B) of the project.
Copy or retype the exact solution you obtained below.
(Name the exact solution s(t))
Now we want to compare the solution obtained by the
rkfiexed routine with the exact values at every step.
Approximate Solution returned by rkfixed
Remark: Notice how the vectorize function is used to
pass the values of t in the first column of S as an
argument to the exact solution s(t).
Compute the absolute value of the maximum error in the
approximate solution.
Hint: The error at a certain step is the difference
between the exact solution and the approximate solution.
g ) The graph of the exact solution is given below
Graph the approximate solution
On the same graph plot both the exact solution and the
approximate solution
Follow the steps below to solve the given IVP over the
interval [
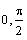
] using the
rkfixed
and
rkadap command.
a) On a piece of paper, use the substitution x0 = x, x1
= x', .... to transform the equation into a system
of first-order differential equations.
Write the derivative vector for the rkfixed command.
b) Define the vector of initial values:
c) Define the initial and final point of the interval
d) For the rkfixed we want to solution to be evaluated
at 51 points, so we use