repeat the above for the 2nd, 3rd and 4th derivatives
Now, to solve for c1, ..., c5 copy the right-hand side
of the symbolic equal (the arrow) into the placeholders
of the vector below. The solve command will be used
to find the values of c1,...,c5
Assign the computed values of c1,..., c5 to the variables
c1, c2, .. c5
(Do not delete.This is used to reset the value of t)
Copy or retype your solution obtained in part (c) below
(Do not substitute the values of c1,...,c5.)
Thus, the particular solution is:
To help you verify that your computation of the constants
c1, .. , c5 were correct, the solution and its derivatives
are evaluated at t = 0 below. They should return the
initial values. If any of the computed values does
not equal to the given initial value, then your computation
of the constants were incorrect.
e) Plot your solution on the interval t = [
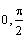
] . Use an increment (stepsize) of 0.01 in defining
the range for t.
<== Define the range values for t here
Remark: Enlarge your graph to fill the width of the
page.
a) Give the characteristic polynomial in terms of the
variable r
b) Use the solve
command to find the roots of the characteristic polynomial.
c) Write the general solution in terms of the constants
c1,.....,c5
The following symbolic computation will verify if your
answer above is correct. It will substitute your solution
into the differential equation and evaluates it symbolically.
If Mathcad returns a zero
(after the arrow) then your solution is correct. Otherwise,
you have to reconsider your solution.
Note: This area is locked so that you can not edit it.
d ) Find a particular solution (evaluate c1, ...c5)
satisfying the initial conditions
To get five equations in the unknowns c1,...,c5, evaluate
the solutions x(t) and its derivatives at t =0 and
equate them to the initial values. The first two equations
are written for you.