b)
Finding a particular solution satisfying the initial
condition:
Display the general solution below
Define the general solution. Use c1, c2 and c3 ( do
not use subscripts).
Define and compute the third solution.
Define and compute the second solution.
Define and compute the first solution. Use the symbolic
equal.
State the condition on v1 for the method to work.
Define v1 using v2 and use the symbolic equal to display
the result.
State the condition on v2 for the method to work.
Define v2 using v3 and use the symbolic equal (the
arrow) to display the result.
Define the components of v3. Use subscripts.
Compute the rref of
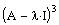
So, the eigenvalue is defective with defect 2 and therefore,
we find v3 by solving the system
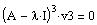
for v3
Based on the rref of
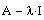
, state how many linearly independent eigenvectors can
be generated by

. Why?
Compute the rref of
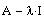
To find the eigenvector associated with
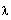
, we solve the homogeneous system
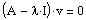
for v. This can be achieved by computing the reduced
row echelon form of the matrix

Since we only have one eigenvalue we can simplify the
computation by assigning the value of
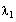
to
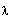
Compute the eigenvalues of A by solving the characteristic
equation for
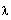
and assigning the vector result to
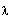
.
Write your observation about relationship between this
char. eqn and the char. eqn of the scalar differential
equation in part A.
Compute the characteristic equation
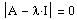
.
Define I as the 3 x 3 identity.
a) finding the
general solution
End of
Part B
End of
Project
End of
Semester
End of
Sufferings
Compare and find the relationship between the solution
of the scalar equation and the solution of the system.
Write your findings below:
The solution of the scalar equation and its derivatives
and the solution of the system are displayed below
for your convenience.
If the two side do not match, it means you have made
a mistake somewhere in your calculations.
Compute the RHS and compare it with the LHS. Use the
simplify command.
Compute the LHS below. Use the simplify
command.
Define the components of the derivative of the solution
as a 3 x 1 vector and name it x'(t).
To verify your solution, you need to compare the left-hand
side x'(t) with the right-hand side Ax(t)
c) Verifying your
solution
Define the general solution (using c1, c2 and c3) one
more time and use the symbolic equal to compute the
particular solution. Use the simplify
command
Define c1, c2 and c3 using subscripts of s (remember
the subscript starts at 1)
Use the solve command to find c1, c2 and c3 and define
the result as s (see step (b3) in part A).
To find a particular solution, we need to find the values
of c1, c2 and c3 by solving the nonhomogeneous system
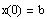
. This is done by equating corresponding components
of the general solution evaluated at 0 and the components
of the initial vector b. That is
1. Compute the first and second derivative of the
solution and define them as y'(t) and y''(t), respectively:
b) To find a particular solution satisfying the given
initial condition, we perform the following steps:
Note: Here we have a root with multiplicity 3 and we
can use any element of the vector r to write the solution.
3. Use the roots (elements of the vector r) to write
the general solution
2. Use the solve
command to find the roots of the characteristic equation
and assign the result to r.
Use the coefficients of the differential equation to
write the characteristic equation in terms of the variable
r
a) To find the general solution we do
a) Find the general solution
b) Find a particular solution satisfying the initial
conditions
Given the homogeneous scalar differential equation:
Part A
This part of the project will be done for you for comparison
with the results to be obtained by you in part B.
Instructions
Carefully fill out the personal information at the top
of this worksheet.
Before you start working on the worksheet, use the "save
as" command to save the
worksheet as follows:
SxxLyyP2
.mcd
where,
xx is your section number
yy is your list number
T
o facilitate the grading of the project, be as neat
as possible and place your input in the space provided
for you.
Unless absolutely necessary, do not add or delete lines
into the document. Enough room is given for writing
your answers.
If for some reason the screen display gets missed up,
press Ctrl+R to refresh the screen.
Frequently save your worksheet to avoid losing of your
work.
You should submit your worksheet in two forms:
a) Softcopy through e-mail
e-mail your worksheet named as explained
in part(8) to
afarahat@kfupm.edu.sa
Do not send a zipped file.
b)
Hardcopy (Print out) to be submitted on or before Wednesday
June 2, 2004.
Collaboration is permitted but
copying in punishable by an F grade.
Objectives
Solve a homogeneous 3rd order scalar differential equation
(the characteristic equation is designed to have a
root with multiplicity 3).
Find a particular solution satisfying given initial
conditions.
Convert the scalar equation into a system of 3 first-order
differential equations.
Solve the system using the eigenvalue-eigenvector method.
Find a particular solution satisfying initial conditions
that are equivalent to the conditions of the scalar
equation.
Verify the solution.
Compare and find the relationship between the components
of the
particular solution of the system and the particular
solution of the scalar equation and its first and second
derivatives
NOTE:
An individual problem will be generated for you using
your section number, your list number and your student
ID number. Therefore, Section_No, List_No, and Student_ID
are defined above as global variables using the global
equal "º
". Use the placeholder to enter the numbers.
If you have any question or need help, e-mail me at
afarahat@kfupm.edu.sa
or call my mobile 050-384-7098. Good luck.
a) Find the general
solution
b)
Find a particular solution satisfying the initial conditions
where A is (Define your coefficient matrix here) ==>
So, given the system of differential equations
On a piece of paper, convert the differential equation
in part A to a first-order system of the form
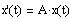
and obtain the coefficient matrix A.
A good source to use for help can be found on the WebCT
(this hyperlink will take you to the logon page of
WebCT). Look for the file
"7.5 P25-m3d2.htm" under "Lecture Notes"
on the webCT page of the course. or my
webpage
(this will take you directly to the file).
In this part, as stated in the objectives, you will
be asked to convert the scalar differential equation,
solved in part A, to a system of first order differential
equations. Then, solve the system using the eigenvalue-eigenvector
method and compare the two solutions. You will also
be asked to find the relationship between components
of the system solution and the solution of the scalar
equation and its derivatives.
For a reason to be found later, we also compute the
derivatives of the particular solution
4. Substitute the computed values of c1, c2, and c3
into the solution to find a particular solution
Note: The solution is stored in a row vector named s.
Therefore, we can assign the values to c1, c2 and c3
as follows:
3. Use the solve command to find c1, c2 and c3
2. Evaluate the solution y(t) and its derivatives y'(t)
and y''(t) at t = 0 and set them equal to the initial
conditions. This will give three equations
in the three unknowns c1, c2 and c3 as computed below: