3-R3+R1
------------>
-R3+R2
c)
Compute the inverse of the coeffic
ient matrix using the adjoint
method.
First compute the cofactors of A a store them in a matrix
B
Property of determinant of products
a) Wri
te the system in the matrix form A x = b.
b) Solve the system using the Gauss-Jor
dan elimination method.
9.
Given the row reduced echelon form of the coefficient matrix
a homogenous
linear system
A
x = 0.
and the adjoint matrix is
d) Solve the system using the inverse method.
Divide by erx
(since erx
never zero)
Compute the integrating factor
NAME:- _________________
St. #: ____________Sec. #: _____
List #: ______
Answer all questions. Show
all your work.
2.
Solve the differential equation in problem (1f).
c) A homogenous system of 3 equations in 3 unk
nowns having no
solution
Impossible. Homogeneous systems are always consistent.
d) A nonhomogenous system of 3 equations
in 4 unknowns having
a unique solution
Impossible. The maximum rank of the reduced matrix is
3 which results in a free variable according to the
formula
Number of free variables = Number of unknowns
- rank
e)
A nonhomogenous system of 4 equations in 3 unknowns having a uni
que solution.
6.
State the conditions under which the linear system
A x
= b can
be sol
ved using the inverse matrix method or Cramerís
Rule.
The inverse-matrix method requires the use of the inverse
of A and Cramer's rule requires the use of the determinant
of A.
Therefore, the two methods can be used if:
A is a square matrix, i.e., the system has equal number
of equations and unknowns,
A must be invertible (which is equivalent to the requirement
the
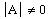
)
5.
If possible (otherwise,
write
Impossible
), give an example of the row reduced echelon form of
the augmented matrix of a linear system with the
following properties:
a) A homogenous system of 4 equations in 3 unkn
owns having a uni
que solution
b) A nonhomogenous system of 3 equations
in 5 unknowns having no solution
If the system is to have no solution, there must be
a leading entry in the last column.