Handoutm6.htm

Introduction

Introduction to Maple

Maple is a language for symbolic mathematical calculation.

Maple statements are input after the > prompt. Every Maple statement must end with a semicolon ; (or a colon : if the result is not to be printed). Until Maple receives a (semi)colon it will neither process the statement nor accept a new statement. If the (semi)colon is forgotten, no further commands will work until a (semi)colon is typed.

Some important Maple functions are
expand , simplify , and normal , which are useful for simplifying expressions;
evalf , for evaluating to floating-point;
solve , for solving equations;
int and diff , for integration and differentiation; and
plot , for plotting functions.

Other useful Maple functions are: array , coeff , collect , convert , degree , denom , evalc , limit , map , normal numer , op , simplify , subs , sum , and type . These commands are the more commonly used ones; this is by no means a complete list of Maple functions. Maple also has many mathematical functions built-in, such as sin , cos , tan , exp , ln , GAMMA , Zeta , and binomial .

The help function can be used to find out more about any Maple function. For instance, to find out about the series command, type series . The Maple assignment operator is := .

The symbols %, %%, %%% indicate the previous, second previous, and third previous expressions in a Maple session.

Examples:

At the beginging of every session, it is a good idea to use the restart command. The restart command will cause the Maple kernel to clear its internal memory so that it acts as if you had just started Maple.

> restart;

adding 3, 5 and 5

> 3 + 4 + 5;

Expand the expression and name the expanded results e1

> e1 := expand( x*(x+1)*(x-1) );

Factor the previous result

> factor( % );

Compute the floating value of

> evalf( sqrt(2) );

Solve the equation 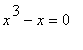(previously called e1) for x

> solve(e1=0, x);

Differentiate 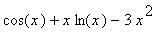with respect to x

> diff(cos(x)+ x*ln(x)-3*x^2,x);

Integrate with respect to x

> int(x*exp(x), x);

To obtain help, use ? followed by a command name

> ?plot;

assign

Function: assign - perform assignments

Calling Sequence:
assign(a, b)
assign(a = b)
assign(t)

Parameters:
a - a name
b - any expression
t - a list or set of equations

Description:

For the cases assign(a,b) and assign(a = b) where a is a name, the assignment a := b is made and NULL is returned. The arguments to assign are evaluated. Hence if b is already assigned the name a, then assign(b,2) would assign a the value 2. Note that b is any valid expression, with one exception: it cannot be an expression sequence containing more than one element.

If the argument is a list or set of equations, then assign is applied to each equation in the list or set.

One use of this function is to apply it to a set of equations returned by the solve function when it is desired to assign the solution values to the variables.

Examples:

One use of this function is to apply it to a set of equations returned by the solve function when it is desired to assign the solution values to the variables.

Solve the linear system for x and y and place the results in a set called s

> s := solve( {x+y=1, 2*x+y=3}, {x,y} );

Now if we type x; or y; Maple does not return the values of x or y. The reason is that the values are not assigned to x and y

> x;

> y;

With the assign command the values are assgind to x and y. So x will have the value 2 and y the value -1

> assign(s);

> x;

> y;

To unassign the values use the command unassign. Note that the variable must be placed between quotation marks.

> unassign('x','y');

Now, x and y will no longer have the values of 2 and -1

> x,y;

See Also: unassign

diff and Diff

Function: diff or Diff - Differentiation or Partial Differentiation

Calling Sequence:
diff(expr, x1, x2, ..., xn)
Diff(expr, x1, x2, ..., xn)
diff(expr, [x1, x2, ..., xn])
Diff(expr, [x1, x2, ..., xn])

Parameters:
expr - an algebraic expression
x1, x2, ..., xn - variables with respect to which differentiation is performed

diff computes the partial derivative of the expression expr with respect to x1, x2, ..., xn, respectively. The most frequent use is diff(f(x),x), which computes the derivative of the function f(x) with respect to x.
The capitalized function name Diff is the inert diff function, which simply returns unevaluated.
The differential operator D is also defined in Maple; see D .

Examples:

> diff(sin(x),x);

> diff(sin(x),y);

The sequence operator $ is useful for forming higher-order derivatives. diff(f(x),x$4), for example, is equivalent to diff(f(x),x,x,x,x)

> diff(sin(x),x,x,x);

> diff(sin(x),x$3);

and diff(g(x,y),x$2,y$3) is equivalent to diff(g(x,y),x,x,y,y,y)

> diff(g(x,y),x,x,y,y,y);

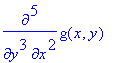
> diff(g(x,y),x$2,y$3);

>

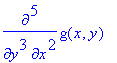
> diff(y^2*x^4,x,x,y,y);

> diff(y^2*x^4,x$2,y$2);

> diff(tan(x),x);

The capitalized function name Diff is the inert diff function, which simply returns unevaluated.

> Diff(tan(x),x);

> Diff(tan(x),x) = diff(tan(x),x);

Since f(x) and f(x,y) are not defined, no evaluation is returned

> diff(f(x),x);
diff(f(x,y),x,y);

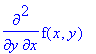
The diff command assumes that partial derivatives commute, that is,

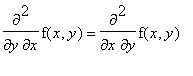
> diff(f(x,y),x,y) - diff(f(x,y),y,x);

These two forms are equivalent:

Variables with respect to which differentiation is performed are given as a list (not inclosed in brackets [ ] )

> diff(g(x,y,z),x,z,z);

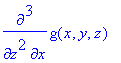
Or, they may be given as a list

> diff(g(x,y,z),[x,z,z]);

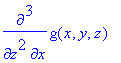
dsolve

dsolve - Solve ordinary differential equations (ODEs)

Calling Sequences:

dsolve(ODE)

dsolve(ODE, y(x), extra_args)

dsolve({ODE, ICs}, y(x), extra_args)

dsolve({sysODE, ICs}, {funcs}, extra_args)

Parameters:

ODE - an ordinary differential equation

y(x) - any indeterminate function of one variable

ICs - initial conditions

{sysODE} - a set with a system of ODEs

{funcs} - a set with indeterminate functions

extra_args - optional, depends on the type of problem being solved (see below)

* Herein {x, y(x)} represent any pair of independent and dependent variables.

Description:

As a general ODE solver, dsolve is able to handle different types of ODE problems. These include:

* looking for closed form solutions for a single ODE (see below) or a system of ODEs (see ? dsolve, system );
* solving ODEs or a system of them with given initial conditions (boundary value problems, see ? dsolve, ICs );
To see what method is being used to solve a given ODE, you can assign the following (see ? infolevel ):

> infolevel[dsolve]:= 0;

INPUT AND OUTPUT

Given an ODE, an extra argument indicating the dependent variable is required only when the given ODE involves more than one function being differentiated. When extra arguments are given, they can be placed in any order after the first one.

Closed form solutions are returned by dsolve as a sequence of explicit (y(x)=F(x,_Cn)) or implicit (F(y(x),x,_Cn)=0) equations, where the _Cn (n=integer) are arbitrary constants. By default, dsolve will return the answer in explicit form, unless solve is not able to isolate the dependent variable.

Integrals appearing in answers returned by dsolve are expressed using the inert Int and Intat (not int or intat ). These integrals will appear when int was not able to calculate them or when it appeared to be convenient not to evaluate them during the solving process. One can request the evaluation of these integrals using the value command.

THE OPTIONAL ARGUMENTS

For the optional arguments in the context of IC problems, systems of ODEs, series or numeric solutions, or the use of integral transforms, see the links to the respective help pages above.
In the case of single ODEs, optional arguments can be given in any order after the first one. A summary of the optional arguments most frequently used is given by:

'implicit' - to avoid dsolve trying to make an answer explicit;
'explicit' - to request answers in explicit form in all cases (provided that solve succeeds in isolating the dependent variable);
'useInt' -to request the use of Int (the inert integral) instead of int during the solving process. This option is useful to speed up the solving process in many cases, and to see the form of the answer before the integrals are performed (pedagogical purposes). To perform the integrals afterwards one can apply the value command to dsolve 's answer.
'class' - to request the use of only classification methods (see ? odeadvisor ) and avoid using symmetry methods.;
'output=basis' - only for linear ODEs, to request the answer as a list of functions that span the solution space. If the differential equation is non-homogeneous, dsolve returns a list containing the list of basis functions followed by a single particular solution.

Examples:

See Also:

odeadvisor , dsolve,algorithms , dsolve,education , dsolve,ICs , dsolve,inttrans , dsolve,formal_series , dsolve,Lie , dsolve,linear , dsolve,numeric ; dsolve,piecewise , dsolve,series , dsolve,system , odeadvisor,types , and the Maple packages for differential equations DEtools , PDEtools

>

Examples:

> unassign('y','x');

> de:=diff(y(x),x$2)-y(x)=sin(x)*x,y(x);

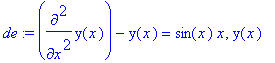
> dsolve(diff(y(x),x$2)-y(x)=sin(x)*x,y(x));

Solve an initial value problem

> dsolve({diff(v(t),t)+2*t=0, v(1)=5}, v(t));

> dsolve(diff(y(x),x) - alpha*y(x) = 0, y(x), explicit=true);

> de1 := diff(y(t),t$2) + 5*diff(y(t),t) + 6*y(t) = 0;

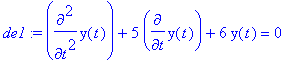
> dsolve({de1, y(0)=0, D(y)(0)=1}, y(t),method=laplace);

> dsolve(diff(y(x),x$2)+2*diff(y(x),x)+6*y(x)=x,y(x),output=basis);

> sys := diff(y(x),x)=z(x)-y(x)-x, diff(z(x),x)=y(x);
fcns := {y(x), z(x)};

> F := dsolve({sys,y(0)=0,z(0)=1}, fcns);

The examples below illustrate the use of dsolve in solving a single ODE. For examples related to more specific problems see: dsolve,initial_conditions , dsolve,system , dsolve,numeric .

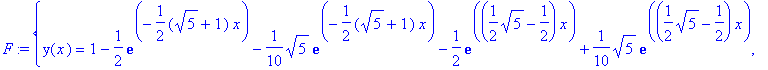
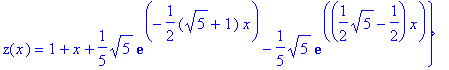
First order ODEs (see ? odeadvisor ).

> ode1 := diff(y(x),x)-y(x)^2+y(x)*sin(x)-cos(x);

> ans1 := dsolve(ode1);

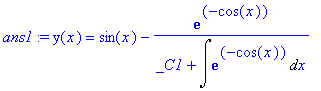
> with(DEtools): odeadvisor(ode1);

ODE of high degree in dy/dx.

A linear ODE

> ode_L := sin(x)*diff(y(x),x)-cos(x)*y(x)=0;

One can indicate to dsolve to use a specific sequence of 'methods' to tackle the ODE. In this example the method for 'linear' ODEs is indicated; in addition the optional argument 'useInt' makes dsolve not evaluate the integral appearing in the answer

> dsolve(ode_L, useInt);

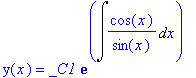
To see the answer before evaluating integrals is useful to understand how the answer was obtained; integrals can be evaluated afterwards using value

> value(%);

Or you can use the dsolve command without specifying the useInt option

> dsolve(ode_L);

This particular linear ODE is also separable

> dsolve(ode_L, [separable], useInt);

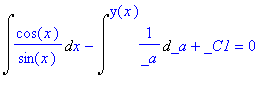
> value(%);

As a general alternative, one can look for an integrating factor (see ? DEtools,intfactor )

> mu := intfactor(ode_L);

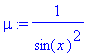
Integrating factors turn ODEs exact; to indicate to dsolve to use the scheme for exact ODEs:

> dsolve( mu*ode_L, [exact], useInt);

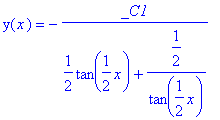
> dsolve( mu*ode_L);

> value(%%);

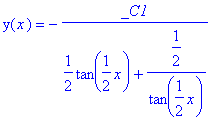
A second order linear homogeneous ODE

> ode4 := diff(y(x), x$2) - x*diff(y(x),x)-
y(x)=0;

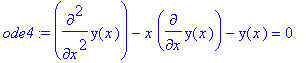
> dsolve(ode4);

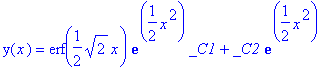
A non-linear second order example

> ode5 := diff(y(x),x,x) =
-1/y(x)^2;

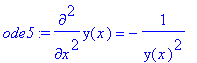
> ans5 := dsolve(ode5);

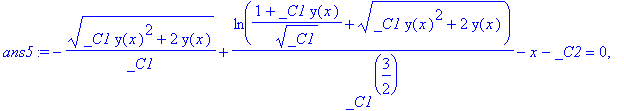
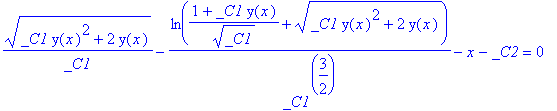
Error, invalid subscript selector

A non-linear high order example solved using symmetry methods:

> ode6 := diff(diff(y(x),x),x)*diff(y(x),x)*y(x)*x^6-
2*diff(y(x),x)^3*x^6+2*diff(y(x),x)^2*y(x)*x^5+y(x)^5;

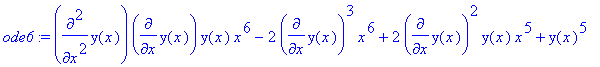
> dsolve(ode6);

>

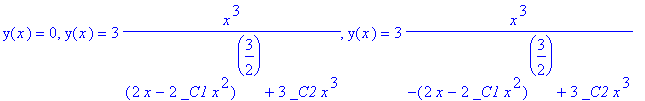
expand

Function: expand - Expand an Expression

Description:

The primary application of expand is to distribute products over sums. This is done for all polynomials. For quotients of polynomials, only sums in the numerator are expanded --- products and powers are left alone. See the normal function for dealing with quotients of polynomials.

expand also knows how to expand most of the mathematical functions, including sin, cos, tan, sinh, cosh, tanh, det, erf, exp, factorial, GAMMA, ln, max, min, Psi, binomial, sum, product, int, limit, bernoulli, euler, abs, signum, pochhammer, polylog, BesselJ, BesselY, BesselI, BesselK, AngerJ, Beta, Hankel, Kelvin, Struve, WeberE, and piecewise.

The optional arguments expr1, expr2, ..., exprn are used to prevent particular sub-expressions in expr (expr1, expr2, ..., exprn) from being expanded. To prevent all functions from being expanded, use the frontend function: frontend(expand,[expr]);

Examples:

> expand((x+1)*(x+2));

> expand((x+1)*(x+3)/(x+2));

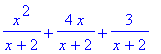
> expand(sin(x+y));

> expand(cos(2*x));

> expand(exp(a+ln(b)));

> expand(ln(x/(1-x)^2));

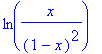
> expand((x+1)*(y+z), x+1);

>

function

Help For: Functional operators

Description:

A functional operator in Maple is a special form of a procedure. Functional operators are written using ``arrow'' notation:
vars -> result

Here, vars is a sequence of variable names (or a single variable) and result is the result of the procedure acting on vars.

For example, the following
x -> x^2

represents the function that squares its argument.

Multivariate and vector functions are also allowed. It is necessary to put parentheses around vars or result whenever they are expression sequences. For example, the following functions have the correct syntax:
(x,y) -> x^2 + y^2
x -> (2*x, 3*x^4)
(x,y,z) -> (x*y, y*z)
Another way to create a functional operator is by using the unapply function. (See the topic ?unapply.)
The semantics of functional operators can best be thought of as a process of ``procedurizing'' the given expression result, since the internal data structure representation is a procedure.
A functional operator of the form:
vars -> result

is semantically equivalent to:
proc(vars) option operator, arrow; result end

Maple performs some automatic simplifications on functional operators (more precisely, on procedures with option operator). For example, x -> sin(x) simplifies to sin.

A constant operator () -> numeric where numeric is a numeric constant, simplifies to just numeric.

The identity operator is expressed as x -> x for any variable name x.

Examples:

Define the function f(x) = 3 x + 5

> f := x -> 3*x + 5;

> f(2);

Define a multivariate function g(x,y) = sin(x) cos(x) + x y

> g := (x,y) -> sin(x)*cos(y) + x*y;

> g(Pi/2, Pi);

Define a vector function

> h := x -> (2*x, x^3);

> h(3);

> h(x);

> k:= x -> linalg[matrix](2,1,[2*x,x^3]);

> k(3);

int

Function: int or Int - Definite and Indefinite Integration

Calling Sequences:
int(expr, x) Int(expr, x)
int(expr, x=a..b, ...) Int(expr, x=a..b, ...)

Parameters:
f - an algebraic expression or a procedure, the integrand
expr - a variable with respect to integration is performed
a, b - the limits of integration for definite integrals
... - options

Description:

The function int computes the indefinite or definite integral of the expression expr with respect to the variable x. The name integrate is a synonym for int.

Indefinite integration is performed if the second argument x is a variable. Note that no constant of integration appears in the result. Definite integration is performed if the second argument is of the form x=a..b where a and b are the endpoints of the interval of integration.

If Maple cannot find a closed form expression for the integral, the function call itself is returned.

The capitalized function name Int is the inert version of the int function, which simply returns unevaluated.

Examples:

> int( sin(x), x );

> Int( sin(x), x );

> int( sin(x), x=0..Pi );

> Int( sin(x), x=0..Pi );

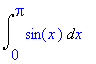
> int( x/(x^3-1), x );

> int( exp(-x^2), x );

Maple is unable to evaluate the following integral

> int( exp(-x^2)*ln(x), x );

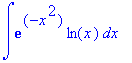
map

Function: map - apply a procedure to each operand of an expression

Function: map2 - apply a procedure with a specified first argument to each operand of an expression

Calling Sequence:
map(fcn, expr, arg2, ..., argn)
map2(fcn, arg1, expr, arg3, ..., argn)

Parameters:
fcn - a procedure or a name
expr - any expression
argi - (optional) further arguments to fcn

Description:

The map function applies fcn to the operands of expr.

The ith operand of expr is replaced by the result of applying fcn to the ith operand. This is done for all the operands of expr.

For a table or array, fcn is applied to each element of the table or array.

If fcn takes more than one argument, they are to be specified as additional arguments, arg2, arg3, ..., argn, which are simply passed through as the second, third, ..., nth arguments to fcn.

The map2 function is similar to map, except that for each operand of expr, arg1 is passed as the first argument to fcn, the operand of expr is passed as the second argument, and arg3, ..., argn are passed as the third, ..., nth arguments.

Note map and map2 do not work well with functions that have special evaluation rules, e.g. evalf.

Examples:

> unassign('f','y');

> map(f, x + y*z);

> map(f, y*z);

> map(f, {a,b,c});

> map(x -> x^2, x + y);

> map(proc(x,y) x^2+y end, [1,2,3,4], 2);

> map2(f, g, {a,b,c});

matrix

Help For: matrices

Description:

A matrix in Maple is represented as a two dimensional array with row and column indices indexed from 1.

Matrices can be input either directly, as a two dimensional array, or using the matrix command in the linear algebra package. For example, array(1..m,1..n); creates an empty m by n matrix. See array and linalg[matrix] for further details.

The i,jth entry of the matrix A is accessed, and assigned to, using the subscript notation A[i,j]. For example, A[i,j] := 1/B[i,j]; assigns the i,j'th entry of the matrix A to be the inverse of the i,jth entry of the matrix B.

The linalg (linear algebra) package includes many matrix operations. See linalg for further information.

The evalm function performs arithmetic on matrices. See evalm for further information.

The map function can be used to apply a function to each entry of a matrix. For example, map(simplify,A) simplifies each entry of the matrix A and map(diff,A,x) differentiates each entry of the vector A with respect to x. See map for further details.

The following indexing functions are available for matrix input: antisymmetric, diagonal, identity, sparse, and symmetric. For example, array(1..10,1..10,identity) creates a 10 by 10 identity matrix.

The linalg package has a number of special matrices. For example, bezout, fibonacci, hilbert, jacobian, sylvester, toeplitz, vandermonde etc. See the linalg package for further details.

See type[matrix] for testing for a matrix. For example, type(A,'matrix(integer)') tests for a matrix of integers.

Examples:

> linalg[matrix](2,3,[x,y,z,a,b,c]);

> array(1..2,1..2,[[1,2],[3,4]]);

> type(%,matrix);

> array(0..1,0..1,[[a,b],[c,d]]):
type(%,matrix);

> A:=linalg[matrix](2,2,[sin(x), x^2+x+3, exp(x), cos(x^2)]);

> map(diff, A, x);

Function: op - extract operands from an expression

Function: nops - the number of operands of an expression

Calling Sequence:
op(i,expr) op(i..j,expr) op(expr) op(list,expr)
nops(expr)

Parameters:
i,j - integers marking positions of operands
expr - any expression
list - a list of integers marking positions of operands at increasing nesting levels of an expression

Description:

The op function extracts components (operands) of an expression. The nops function returns the number of operands of an expression.

If the first argument to the op function is a positive integer i then the result is the ith operand of expr. If the operand does not exist, an error occurs.

If the first argument to op is a range i..j then the result is a sequence of the ith to jth operands of expr.

If there is only one argument to the op function, this is equivalent to op(1..nops(expr),expr).

If the first argument to op is a list list, the elements of the list refer to a sub-operand of expr at increasing levels of nesting. The expression op([1,3],expr) returns the 3rd operand of the first operand of expr

op(1,expr) yields expr.

Examples:

Define a list of three elements (operands)

> u := [1,4,9];

> nops(u);

> op(2,u);

> op(2..3,u);

> op(u);

> op(0,u);

> [op(u),16];

> v := f(x,y,z);

> nops(v);

> op(0,v);

> op(2,v);

> op(4,v);

Error, improper op or subscript selector

> op(v);

> w := f(g(a,b),h(c,d));

Retrun the 2nd operand of the first operand of w

> op(1,op(2,w));

The same as above but clearer

> op([2,1],w);

restart

start over, (almost) as if Maple were restarted

Calling Sequences:
restart;

Description: :

The restart command will cause the Maple kernel to clear its internal memory so that it acts as if you had just started Maple.

The settings of all identifiers (variables and procedures) will be forgotten, libname will be reset to the state it was in when Maple was started, loaded packages will be unloaded, and the Maple initialization files will be reread.

Examples:

> a := 2;

Load the differential equation tools package

> with(DEtools):

Define a 2nd order DE in stanadard form de:=diff(y(x),x$2)+p(x)*diff(y(x),x)+q(x)*y(x)=0;

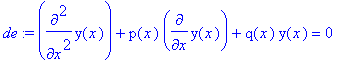
Use the reduceOrder command supplied with the DEtools package (given a solution y[1](x), find another solution y[2](x)

> y[2](x):=reduceOrder(de,y(x),y[1](x));

Restart Maple

> restart;

The value of a is no longer known

> a;

The command reduceOrder is no longer knows

> y[2](x):=reduceOrder(de,y(x),y[1](x));

See Also: unassign

sets and lists

Help For: Sets and lists

Calling Sequence:
{es}
[es]

Parameters:
es - an expression sequence

Description:

A set is an unordered sequence of distinct expressions enclosed in braces, representing a set in the mathematical sense. The user should not assume that the expressions will be maintained in any particular order because Maple uses an ordering convenient for its implementation.

A list is an ordered sequence of expressions enclosed in square brackets. The ordering of the expressions is the ordering of es.

Note that es may be empty so that the empty set is represented by {} and the empty list is represented by [].

The elements of a set or list may be extracted via the selection operation. Thus, if S is a set or list then the ith to jth elements of S can be obtained by: S[i..j] or equivalently, op(i..j,S). Negative selectors can also be used. The -1th element is the last, the -2th the second last, and so on.

Appending an element x to a list L is done by [op(L),x]. Inserting an element x to a set S is done using the union operator S union {x}.

Replacing the i-th element of a list L by x can be done by subsop(i=x,L). Deleting the i-th element of a list L is subsop(i=NULL,L). Deleting an element x from a set S is done using the minus operator S minus {x}.

Examples:

> {x,y,y};

> {y,x,y};

> [x,y,y];

> [y,x,y];

> L := [seq(x[i],i=1..4)];

> L[2];

> L := [op(L),x[5]];

> L[-3..-2];

> L := subsop(2=NULL,L);

simplify

Function: simplify - Apply Simplification Rules to an Expression

Calling Sequence:
simplify(expr)
simplify(expr, n1, n2, ...)
simplify(expr, assume=prop)

Parameters:
expr - any expression
n1, n2,... - (optional) names or sets or lists
prop - any property (optional)

Description:

The simplify function is used to apply simplification rules to an expression. If only one argument is present, then simplify will search the expression for function calls, square roots, radicals, and powers. Next it will invoke the appropriate simplification procedures, which include: exp, ln, sqrt, polylog, trig (for trig functions), radical (occurrence of fractional powers), power (occurrence of powers, exp, ln), and atsign ("@") (for operators).

In the case of two or more arguments where the additional arguments are names, simplify will only invoke the simplification procedures specified by the additional arguments.

Whenever the last argument is assume=prop, all the indeterminates in expr are assumed to have the property prop to compute the simplified expression.

Examples:

> expr1:=4^(1/2)+3;

> simplify(expr1);

> expr2:=exp(a+ln(b*exp(c)));

> simplify(expr2);

> expr3:=sin(x)^2+cos(x)^2;
simplify(expr3);

> e := cos(x)^5 + sin(x)^4 + 2*cos(x)^2 - 2*sin(x)^2 - cos(2*x);
simplify(e);

> f := -1/3*x^5*y + x^4*y^2 + 1/3*x*y^3 + 1;
simplify(f, {x^3 = x*y, y^2 = x+1});

> g:=sqrt(x^2);

> simplify(g);

> simplify(g,assume=real);

> simplify(g,assume=positive);

solve

Function: solve - Solve Equations

Calling Sequence:
solve(eqn, var)
solve(eqns, vars)

Parameters:
eqn - an equation or inequality
eqns - a set of equations or inequalities (equations or inequalities enclosed between braces {})
var - (optional) a name (unknown to solve for)
vars - (optional) a set of names (unknowns to solve for) (unkowns enclosed between braces {})

Description:

The solution to a single equation eqn solved for a single unknown var is returned as an expression. To solve a system of equations for some unknowns the system is specified as a set of equations eqns and a set of unknowns vars. The solutions for vars are returned as a set of equations.
The output from solve in general is a sequence of solutions. In the case of multiple solutions, you should put the solutions in a list or set before manipulating them further. When solve is unable to find any solutions, the empty sequence NULL is returned. This means that either there are no solutions, or simply that solve was unable to find the solutions.
Two shortcuts for the input of equations and unknowns are provided. Wherever an equation is expected, if an expression expr is specified then the equation expr = 0 is understood. If vars is not specified, Maple will solve for all the variables that appear in eqns.
In general, explicit solutions in terms of radicals for polynomial equations of degree greater than 4 do not exist. In these cases, implicit solutions are given in terms of RootOfs. Note that explicit solutions for the general quartic polynomial equation are not by default given because they are too complicated and messy to be of use. By setting the global variable _EnvExplicit to true then solve will return explicit solutions for quartic polynomials in all cases. By setting _EnvExplicit to false, all solutions which are not rational will be reported as RootOfs.
When abs is used in the context of solve, solve assumes that the argument to abs is real-valued.
For solving differential equations, use dsolve. For purely floating-point solutions use fsolve. Use isolve to solve for integer solutions, msolve to solve modulo a prime; rsolve for recurrences, and linalg[linsolve] to solve matrix equations.
Further information is available for the subtopics solve[subtopic] where subtopic is one of

floats functions identity ineqs linear
radical scalar series system

For systems of polynomial equations, the function grobner[gsolve] which uses a Grobner-basis approach may be useful.

Examples:

> restart;

Solve for a

> solve( f=m*a, a );

Solve eq for x

> eq := x^4-5*x^2+6*x=2;
solve(eq,x);

Solve eq for x and put the answers in a list (brackets). This way we can refere to the solutions as elements of the list

> sols := [solve(eq,x)];

Element i in the list is refered to as sols[i].

> sols[1];sols[3];

Use evalf to converst the answers to floating points

> evalf(sols);

> eq;

Solve eq for x and put the answers in a set (braces). We can then refer to the elemenst using subscripts.
Note that the repeated root was not listed twice as was the case in putting the answers in a list (see above)

> sols := {solve(eq,x)};
sols[1];sols[3];

Check the first answer by substituting it in the equation

> subs( x=sols[1], eq );

> simplify(%);

Equations are provided in a set, no set of unknowns is provided (hence Maple assumes that we are solving for the variables in the equations):

> eqns := {u+v+w=1, 3*u+v=3, u-2*v-w=0};

Manipulating Solutions solve for u,v,w

> sols := solve( eqns );

check solutions

> subs( sols, eqns );

pick off one solution

> subs( sols, u );

assign all solutions

> assign( sols );
u;w;

Other examples

> solve( cos(x)+y = 9, x );

> solve( x^2+x>0, x );

Solve a system of equations

> solve( {x^2*y^2=0, x-y=1} );

> solve( {x^2*y^2=0, x-y=1, x<>0} );

unapply

Function: unapply - Returns an Operator from an Expression and Arguments

Calling Sequence:
unapply(expr,x,y,..)

Parameters:
expr - any expression
x,y,.. - variable names

Description:

The result of unapply(expr,x) is a functional operator. Applying this operator to x gives the original expression.
unapply(expr,x)(x) ==> expr

In particular, for a function f(x),
unapply(f(x),x) ==> f

unapply should be used whenever it is desired to construct an operator using contents of variables or evaluated expressions.

Examples:

> p := x^2 + sin(x) + 1;

> f := unapply(p,x);

> f(Pi/6);

> q := x^2 + y^3 + 1;

> f := unapply(q,x);

> f(2);

> g := unapply(q,x,y);

> g(2,3);

with

Function: with - loads a library package such as DEtools, linalg, etc

Description:

If only the name of the package is supplied to with then all the functions in the package will be defined. Additional arguments (if present) restrict the defining process to the specified functions. These may be specified individually, or as a list of function names.

Packages are usually defined directly by a name table. The indices of the name table are the short names, while the entries of the table are the actual procedures or readlib references.

The procedure with returns a list of the functions it defined.

Examples:

Define a 2 x 2 matrix

> a:=matrix(2,2,[1,2,3,4]);

The inverse of the matrix in not computed because the inverse command resides in the package linalg which has not been loaded yet

> inverse(a);

Load the linear algebra package. The commands that are available in the package are listed (if you do not want to see the list of availabe commnads terminate the with command with ' : ' instead of ' ; ')

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

Now the inverse command is availabe and the inverse of a is computed

> inverse(a);

wronskian

Function: linalg[wronskian] - wronskian matrix of a vector of functions

Calling Sequence:
wronskian(f, v)

Parameters:
f - a vector or list of expressions
v - a variable

Description:

The procedure wronskian(f, v) computes the wronskian matrix of f with respect to v. The (i,j)-th entry of the matrix result is diff(f[j],v$(i-1)). The wronskian determinant is the determinant of the wronskian matrix.

The command with(linalg,wronskian) allows the use of the abbreviated form of this command.

Examples:

> with(linalg):

> A := vector([exp(x),cosh(x),sinh(x)]);

> Wr := wronskian(A,x);

> det(Wr);