In the above example we extracted a submatrix from row
1 to row 2 and from column 2 to column 3
Thus, to extract a row of a matrix we use the submatrix
command. For example to extract the second row of matrix
A above we use
Note: The command cols( ) is used so that we get all
the columns of the matrix.
Another way to get a row of a matrix is to first transpose
the matrix then use the Matrix Column command
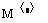
and then transpose again
. For example, the second row of matrix A is obtained
as follows:
Use the augment( )
command to join tow matrices horizontally (side by
side)
Use the stack( )
command to join two matrices vertically (one on top
of the other)
Use the rref( )
to computer the reduced row echelon form of a matrix
Use the rank( )
command to compute the rank ( = the number of nonzero
rows) of a matrix
Use the identity( )
command to create a 3 x 3
identity matrix
Use the rows( )
command to find the
number of rows in matrix A
Use the cols( )
command to find the
number of columns in matrix A
Use the
Matrix Column
command
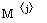
to
extract column j of the matrix
key: A ctrl 6 then type the column number in the
place holder
Or type A then use the Vector and Matrix Palette and
click on
Note: Mathcad does not have a command to extract a row
from a matrix, but it can be done in an indirect way
as will be shown later.
Use the command submatrix(
) to extract a
submatrix of a matrix
The command format is a follows:
submatix(matrix name, from_row, to_row, from_column,
to_column)
Note: Unlike vectors, no subscripts are assigned to
the variable x
Mathcad will not display
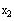
since x is not
subscripted.
Create a range variable y from 2 to 3 with increment
0.2
In general, a set of values in the closed interval [a,
b] with increment incr can be created by
Create a range variable z from 10 to 6 with decrement
0.5
(Or
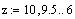
)
Create a diagonal matrix D whose diagonal elements are
all -3
Other ways to define a matrix
A matrix can be defined by assigning values to its elements
Notice that the elements that were not assigned values
are set to 0 by Mathcad
A 3 x 2 matrix with all elements equal to 0 is created
by
A variable with incremental values can be created by
what Mathcad calls "range variable". For
example, a variable x with values 1, 2,3 ...10 is created
as follows:
Or type x : 1 then use the Arithmetic Palette and
choose Range Variable
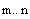
Note that the fist element of the vector is named
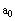
not
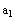
To force Mathcad to start the subscription from 1 rather
than zero, we type the keyword: ORIGIN and assign the
value 1 to it (we only have to do this once at the
beginning of the worksheet.)
Now
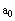
is not defined and
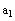
will be the name of the first component of the vector
From now on all subscripts of vectors and matrices will
start from one.
Create two vectors a and b
Multiply the vector a scalar 2
Compute the length of a vector
Introduction to Mathcad Vectors and Matrices
Mathcad uses 0 as the first subscript of vectors and
matrices. For example, to create a 3 x 1 vector type
the name of the vector then press the colon ":"
key then press Control M. choose the number of rows
(3) and columns (1). You get
keyboard keys: a : ctrl m (or use the Vector and Matrix
Palette then click on the icon Matrix or Vector)
Fill in the place holders "
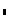
" with the values of the vector's elements
Display the elements of the vector
keyboard keys: a [ 0 =
Or type a then use the Arithmetic Palette and click
on
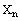
key: B ctrl 1
or use the Vector and Matrix Palette and choose
Matrix Transpose
Note: This is not B to the power T
Compute the product BA and define it as P
Compute the determinant
of P
key: | then type the name of the vector
and press =
Or type P then use the Vector and Matrix Palette and
click on | x |
Compute the inverse
of the P
Use the diag( )
command to create a diagonal
matrix with vector v as its diagonal.
key: | then type the name of the vector
and press =
Or type P then use the Vector and Matrix Palette and
click on | x |
Another way to compute the length of a vector (using
the definition)
Create a 3 x 2 matrix A and a 2 x 3 matrix B
Multiply Matrix A by a scalar
Every element is multiplied by 3
Compute the transpose
of the matrix B