Given the initial condition x(0) = b, where
If an initial condition was given for the system above,
then the problem becomes an initial value problem and
we have to evaluate the constants c1, c2 and c3 in
the general solution.
Then we compute A x(t) and
compare it to x'(t).
To verify that x(t) is a solution to
the system x'(t) = A x(t), we first
define the derivative of the
solution
Verification of the solution
The general solution
is formed
using the above solutions
We define a third solution using the
above e-vector
Thus, the second e-vector associated
with
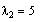
is
Note: Mathcad requires
a redefinition of x(t)
and the general solution
reduces to
the particular
solution
Compute the reduced row
echelon form of Xb
Form the augmented matrix
and name it Xb
To solve such a nonhomogeneous system we form the augmented
matrix
[x1(0)
x2(0) x3(0) | b ]
and compute the row reduced echelon form as follows
Such a system can rewritten as X c = b
where X = [x1(0) x2(0) x3(0)
] and c =

Now, to find c1, c2 and c3 we need to solve the nonhomogeneous
linear system
So, we have one free variable

Compute the row reduced
echelon form of
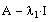
This can be achieved by computing the reduced row echelon
form of the coefficient matrix
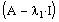
.
To find the e-vector associated with
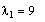
, we need to solve the homogeneous system
Case

Compute the e-values
by finding the roots of the
characteristic equation
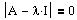
Define I as the 3 x 3 identity
matrix
Solve the system of differential equations
This is a example of solving a homogeneous system of
differential equations with a
non-defective eigenvalue of
multiplicity 2.
To get a second e-vector we choose
We use this e-vector to define
the second solution
With these choices we get
the first e-vector associated
with
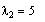
Here we have two free variables v
3
and v
2
which means that we can generate two linearly independent
e-vector associated with
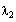
.
Compute the row reduced
echelon form of
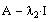
Again, to compute the e-vector associated with
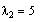
we compute the rref of
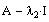
Case
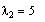
Using the definition the first solution
Thus, the e-vector associated with
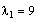
is