Form of the particular solution
First derivative of partic. soln
Substitute in the diff eqn
Equate coefficients of similar terms
Using Mathcad to solve for A and B
So, we can solve for A and B. But what about C?.
The coefficient C can not be determined because the
term
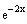
appears in both the nonhomogenus term and the complementary
solution.
Example
Solve the diff eqn
The terms and derivatives of the nonhomog functions
are
Non appear in the complementary solution. Therefore
the form of the particular solution is
CASE 2
(The terms of f(x) or its derivatives appear in the
complementary solution)
Roots of the charac. poly
1 , x and
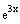
Nonhomgenous terms and their derivatives
So the general solution is given by
Example
If the roots of the characteristic poly of the diff
eqn
are 4, 4, 4 , 2i, -2i. Find the form of the complementary
solution of the diff eqn
Particular solution before modification
Since
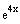
appears in the complementary solution with multiplicity
3, so we multiply
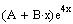
by

. Similarly the cos 2x and sin 2x appear in the comp
solution with multiplicity 1. so we multiply the terms
of the sin and cos by x.
Thus, the modified particular solution is
If we ignore the fact that the term
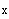
appears in the complementary solution, then the particular
solution will have the form
To avoid duplicating the terms that appear in the complementary
solution
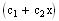
we multiply the corresponding terms in y
p(x) by
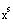
,
where s is the multiplicity of the root that produced
the duplicated
terms (in this case 2) (See the justification page 330
in text)
Thus, we modify
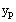
by multiplying it by
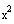
Substitute the derivatives in the diff eqn gives
The above eqn says that every other solution of the
nonhomogenous eqn is the sum of the associated solution
of homogenous eqn and a particular solution of the
nonhomogenous eqn.
Thus, to find the general solution of the nonhomogenous
eqn we first solve the associated homogenous eqn and
try to find one particular solution of the nonhomogenous
eqn.
Method of Undetermined
Coefficients
This method will work of nonhomogenous linear diff.
eqns with constant coefficients with the nonhomogenous
term f(x) that are linear combinations of products of the functions
1. polynomials in x
2. erx
3. cos(bx) and sin(bx)
The method of solution depends on wither the terms of
the function f(x) or any of their derivatives appear
in the solution of the associated homogenous eqn.
CASE 1
(non of the terms of f(x) or their derivative appear
in the solution of the homog. eqn)
Example
Solve the diff eqn
The associated homog. eqn.
5.5 Undetermined Coefficients and Variation of Parameters
The general nonhomog linear diff. eqn has the form
with the associated homogenous eqn
Then eqn (1) can by written as
The operator L defined in (3) is a linear operator.
That is
Let
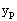
be a particular solution of the nonhomogenous eqn (1),
i.e.,
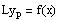
. If y is any other solution of eqn (1), i.e.,
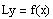
then
This means that the difference of the two solutions
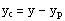
is a solution of the associated homogenous eqn. (2)
Therefore, when substituting in the form of the particular
solution
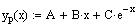
, we get
And the general solution is given by
Example
Find the form of the particular soln of the diff eqn.
Roots of the charac. poly.
Roots of the characteristic eqn.
The complementary solution
The terms and their derivatives of the nonhomogenous
function f(x) =3x - 2 e-x
are
Note that non of them appear in the complementary solution.
Therefore, let us try a particular solution of the
form
where A and B are coefficient to be determined by substituting
in the diff Eqn.
Substitute in the diff. eqn.
Equating the coefficients of similar terms gives