Theorem 4.4.2

If S and T are two bases for a vector space V, then

Thus, S does not span R4 even though the vectors in S are linearly independent.

However, we can not express the vector as a linear combination of the given vectors.

These vectors are clearly linearly independent in R4.

Consider the set

Question: Is it possible for a set to be linearly independent and not span a vector space?

Answer: Yes (see example below).

Example 4.4.7

Thus, the vectors span R3 even though they are linearly dependent.

be a vector in R3 . Then w can be written as a linear combination of

the vector in S as follows

Let

Then S is linearly dependent since it contains more than 3 vectors.

be a set in R3

Let

Question: Is it possible for a set to span a vector space even though it is not linearly independent?

Answer: Yes (see example below).

Example 4.4.6

Check:

and

Theorem 4.4.3

Let S be a subset of an n-dimensional vector space V. Then

a) If S is linearly independent and it has n vector then S is a basis for V

b) If S spans V and it has n vectors then S is a basis for V

c) If S is linearly independent, then it must be a subset of some basis for V

d) If S spans V, then it contains a basis for V.

The following theorem relates the ideas of linear independence, spanning sets, and basis for a vector space.

Here we have number of leading entries = 2 and number of vectors = 2

Therefore, they are linearly independent and they form a basis for the solution space W.

That is, v1 and v2 span the solution space, and we have W = span {v1, v2 } . Now, for the two vectors to be a basis for W, they must be linearly independent To find out if they are linearly independent or not, we compute the rref [ v1 v2]

Therefore, all solutions of the system are linear combinations of the vectors

==>

Let x2 = s and x4 = t ==> x1 = - 2 x2 + 2 x4 = - 2s + 4t and x3 = 0

Thus, x2 and x4 are arbitrary

Compute the rref (A)

Example 4.4.5

Find a basis for the solution space of the linear system A x = 0, where

Recall that the solution space W of the homogenous system A x = 0 is a subspace of the vector space Rn . If the system has only the trivial solution then W = {0}.

If the system has infinitely many solutions then we look for a bases for the subspace W such that all solutions of the system can be expressed as a linear combination of the the bases vectors.

Bases for Solution Spaces of homogenous systems

Remark

Recall that V = {0} is a vector space (by the definition of a vector space)

In this case dimV = 0 since V has no linearly independent set of vectors.

dimRn = n since there are n vectors in any basis for Rn

Definition 4.4.2

The number of vectors in a basis for a vector space V is called the dimension of V and is

denoted by dimV. If the number of vectors in the basis is finite then the vector space is called a finite-dimensional vector space, otherwise it is called an infinite-dimensional vector space.

Example 4.4.4

number of vectors in S = number of vectors in T

Form a matrix A with the given vectors as columns

To show that the vectors form a basis, we only need to show that they are linearly independent (using Theorem 4.4.1).

form a basis for R3.

Example 4.4.2

Show that the vectors

Theorem 4.4.1

Any set of n linearly independent vectors in Rn forms a basis for Rn

Proof

Let S = {v1, v2, ...., vn } be a set of n linearly independent vectors in Rn

Since they are linearly independent we only need to show that they span Rn

Let w be a vector in Rn and recall the theorem that says any set of more than n vectors in Rn is linearly dependent. Thus, the set {w, v1, v2 , ...., vn } is linearly dependent.

==> there are constants c, c1 , c2,...., cn not all zeros such that

cw + c1 v1 + c2 v2 + .....+ cn vn = 0

The constant c could not be zero, otherwise there should be another constant not equal to zero and this will lead to the conclusion that the vectors v1, v2 ,... , vn are linearly dependent ( contradicting our assumption).

Since c ¹ 0, we can divide by it to solve for w:

.

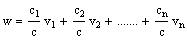
Thus, any vector w in Rn can be written as a linear combination of the vectors v1, v2, ...., v n.

==> S spans R n.

The set { e1, e2, ...en } is called the standard basis for Rn.

This shows that any vector in Rn can be written as a linear combination of the these vectors. Thus, they span Rn

2. Let be any vector in , then w can be written as a linear combination of the vectors

e1,e2, ..., en as follows:

w = w1 e1 + w2 e2 + ....+ wn en

form a basis for the vector space R n because:

1. The vectors are linearly independent ( det [v1, v2 , ..., vn] = 1 ¹ 0 )

The standard unit vectors

<-- jth row

Example 4.4.1 (standard bais for Rn )

That is, every vector w in V can be written uniquely ( because of the linear independence of the vectors) as a linear combinations of the vectors in S. If w is a vector in V, then there are constants c1, c2 , ..., ck, such that

w = c1 v1 + c2 v2 + .....+ ck vk

These constants are unique in the sense that w can not be written in any other way.

Definition (basis )

A set S = {v1, v2, ..., vk } of vectors in a vectors space V is called a basis if

a) the vectors in S are linearly independent

b) the vectors span V.

4.4 Bases and Dimension of Vector Spaces:

Thus,

Compute the reduced row echelon form

Form the augmented matrix of v1 , v2, v3 and w

where A = [v1 v2 v3] and

To express w as a linear combination of the vectors v1, v2, v3 we need to find the constants c1, c2 and c3 such that

w = c1 v1 + c2 v2 + c3 v3

That is, we need to solve the nonhomogeneous linear system A c = w

Example 4.4.3

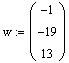
Express the vector as a linear combination of the vectors in the previous example.

Question: Can you think of another way to show that the vectors form a basis for R3?

Since the rank of A is 3 and the number of vectors is 3 ==>

number of free variables = 3 - 3 = 0

That is, there are no free variables ==> the system A c = 0 has only the trivial solution ==> the

vectors are linearly independent ==> they form a basis for Rn.

(using Mathcad rank( ) command)

Another way to find if the vectors are linearly independent or not is to compute the rank of A and compare it with the number of vectors (columns of A)

The reduced matrix has 3 leading entries which is equal to the number of vectors. Thus the linear system A c = 0 has only the trivial solution

==> the vectors are linearly independent ==> the vectors form a basis for R3 .

Compute the reduced row echelon form of A

Compute the reduced row echelon form of A

Result of the augment command

Augment the vectors in a matrix named A