We now substitute the computed integral into equation
(2)
(Reset the variable y to erase the previous definition
of y))
Example 4
Solve the differential equation
Solution
Rewrite in the standard form
Thus, by substituting for t in (3), we get
In general
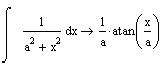
The same substitution is used in the integral
(try to compute it yourself)
(Use symbolic equal to compute the value of the integral)
Example 2
Solve the initial value problem
Rewrite the equation in normal form
1.2 First -Order Differential Equations.
Recall that the normal
form of the first order differential equation is
If it happens that the function f(x,y) is a function
of x alone
, then equation (1) takes the form
In this case the differential equation can easily be
solved by direct integration with respect to x
Remark:
Solving these types of differential equation is not
all that difficult. So, the many examples given below
should be taken as a review of integration techniques.
Each integration is carried out in details and Mathcad
is used, whenever possible, to check out the integration
results.
Example 1
Solve the differential equation y' = 3 ( 5x + 4)20
The substitution method is used to find the integral
Example 3
Solve the differential equation
Again we integrate by parts. However, it is best to
first compute the integral and then substitute the
result.
Combine the integral on the right with the one on the
left
As discussed in class, we use the table below to perform
successive integration by parts
So, the sulution is computed as
To get a particular solution, we use the initial condition
to evaluate the constant C.
Therefore, the particular solution is given by