Define
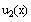
and compute symbolically.
Define the particular solution as

and compute it symbolically.
The step below is provided to verify that the particular
solution satisfies the differential equation.
_____________O_____________
3. Given that
1, -1, -1, 1+ i, 1 + i are the roots of the characteristic
polynomial of a linear homogenous differential equation
with real constant coefficients L y(x) = 0
a) Find the operator L using the
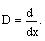
notation.
Note:
You may leave L in a factored form but make sure that
it does not involve complex numbers.
Define the operator L using the given roots.
Note: The fact that the differential equation has only
real coefficient means that complex roots appear in
conjugates.
Use the "expand" command to display the operator
L.
Remark: L may also be defined in the following manner
b) Write the general solution of the differential
equation.
_____________O_____________
4. Given the linear
system
a ) Find a basis for the solution space of the system
The system will be solved by the "Given .. Find
( )" command.
Extra:
We may check if we got the right answer as follows:
Define y'(x) and y''(x) as the first and second derivative
of y(x), respectively and evaluate symbolically to
see the computed derivatives.
Substitute in the left-hand side of the differential
equation and use the "expand" command. The
answer should be equal to the right-hand side of the
equation.
_____________O____________
2. Given that
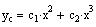
is the complementary solution of the differential equation
find a particular solution of the equation using the
method of variation of parameters.
Define the two solution of the associated homogeneous
equation as y1(x)
and y2(x).
Define the nonhomogeneous term as f(x) after dividing
the equation by the coefficient of the highest derivative.
Define the Wronskian matrix as W(x) and evaluate symbolically
to display the result.
Compute the Wronskian as the determinant of W(x) and
evaluate symbolically.
Define
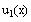
and compute symbolically.
Define two vectors u an v elements in the vector space
V. Apply the condition on their components.
Compute the sum u + v, symbolically.
The sum vector satisfies the conditions on the components
of the elements of V. Therefore, V is closed under
addition.
Make the decision whether V is closed under addition
based on whether the components of the sum vector satisfies
the conditions.
Compute a scalar (k) multiple of a vector in v and make
the decision whether V is closed under scalar multiplication
based on whether the components of kv satisfies the
conditions.
The components of a scalar multiple of a vector in V
satisfies the conditions. Therefore, V is closed under
scalar multiplication.
Therefore, V is a subspace of R4
.
_____________O_____________
6.
Justify without solving that the vectors
We have for vectors in R3
. Therefore, using the theorem that states: "any
n + 1 vectors in Rn
are linearly dependent," the vectors are linearly
dependent.
_____________O_____________
7.
Answer the following questions with (T)rue or (F)alse.
Penalty: An incorrect answer will cancel a correct
answer.
____T____ In an n-dimensional vector space V, a vector
in V can be written in one and only one way as a linear
combination of a set of n linearly independent vectors
in V.
____F____ The dimension of a vector space V is the number
of elements in V.
____F____ In an n-dimensional vector space, a set of
n-1 vectors must be linearly dependent.
____T____ Every subspace of a vector space contains
the zero vector.
____T____ If a set S spans the vector space V, then
S contains a bases for V.
____F____ Any set of vectors that spans a vector space
V must be linearly independent.
____F____ Any linearly independent set of vectors in
Rn forms a basis for Rn
____F____ If a set S in a vector space V is linearly
independent, then it contains a basis for V.
____T____ The principle of superposition states that
if x and y are two solutions to a homogeneous system,
then any linear combination of x and y is also a solution
to the system.
____T____
The solution space of a homogeneous linear system of
3 equations in 4 unknowns is a subspace of R4
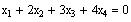
Copy the equations given above and enclose them between
the keywords Given and Find(var
1
, var
2,....),
where
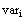
stands for the variable names you are solving for.
Use symbolic evaluation to find the solution.
Note: Another way to solve the system is to use the
"solve" command as show below.
To get the basis vectors, separate the solution vector
along the free variables.
Thus, the basis vectors are
b) Justify (without computation) that the basis
vectors are linearly independent.
They are linearly independent because one is not a scalar multiple of the
other.
c) What is the dimension of the solution space?
Why?
The dimension of the solution space is 2 since the basis
contains 2 vectors.
_____________O_____________
5.
Let V be the set of all vectors in
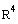
such that: if v =
 e
e
V, then
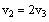
and
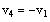
. Show that V is a subspace of
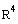
.
This is used to reset the variable
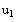
since it was assigned a value before.
Let u an v be two vectors in V, then
Define the two solutions as y1
(x) and y2
(x) in terms of the roots r1
and r2
, then use the symbolic evaluation to display the two
solutions.
Define the Wronskian matrix as W(x) and evaluate symbolically
to display the results
Compute the determinant of W(x) to find the Wronskian
of the two solutions. Use the "simplify"
command to simplify the result.
Because the exponential function
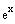
is never zero, t
he two solutions are linearly independent for all real
values of x.
e) Give the interval over which the two solutions
of the homogeneous equation are linearly independent
All real numbers since ex
is never zero.
f) Use following steps to find the general solution
of the nonhomogeneous equation using the method of
undetermined coefficients:
f1. Write the unmodified form of the particular solution
f2. Write the modified form of the particular solution
yp(x)
The exponential term is multiplied by x because it appears
in the complementary solution due to the root "2"
having multiplicity 1.
f3. Compute the first and second derivative of yp(x)
Define the first derivative as y'p
(x) and evaluate symbolically to display the computed
derivative.
Define the second derivative as the derivative of the
first derivative and evaluate symbolically.
Note: You may also compute y''p
(x) using the second order derivative of yp(x).
Answer all questions, show
all your work!
Remark:
The exam is solved, in most part, using Mathcad.
The first problem was designed and solved so that it
can be used as a template for the computer project.
Each step of the solution is commented. Comments on
steps displaying long results are placed in the middle
of the page rather that to the right
1.
Execute the following steps to find a solution to the
differential equation
satisfying the initial conditions
a) Write the associated homogeneous equation
b) Find the roots of the characteristic equation
Define r as the auxiliary equation and use the "solve"
command to find the roots. This way the results will
be assigned to r as a vector and the solutions can
then be referred to using vector subscripts of r.
Display the roots using subscripts of r.
c) Write the complementary solution
Define the complementary solution as
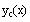
and evaluate symbolically to display the solution with
the roots substituted by Mathcad.
d) Show that the two solutions of the homogeneous
equation are linearly independent. Justify your answer
Define the derivative of y(x) as y'(x) and evaluate
symbolically.
Evaluate the first derivative at the initial point and
set it equal to the given initial value, then evaluate
symbolically to get the second equation of the linear
system.
g3. Write the linear system obtained in parts (g1) and
(g2) as a matrix equation A c = b
This has to be done manually, but it can be automated
using the "Given.. find" command.
g4) Form the augmented matrix of the system above
g5) Compute the reduced row echelon form of the augmented
matrix to solve the system
g6) Give the values of the constants c1 and c2 found
above
Define
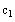
and
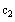
based on the solution found in the previous step.
g7) Substitute the above values in the general solution
of the nonhomogeneous equation to obtain the particular
solution
Redefine the complementary solution as you did in part
(c). This is required by Mathcad since the earlier
definition of
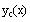
was given before the c's were defined.
Redefine the general solution in terms of

and

(for the same reason as above).
Display the general solution. This will give the particular
solution with the constants substituted in the general
solution.
f4. Substitute yp
and its derivatives in the nonhomogeneous equation,
simplify, and equate similar terms to determine the
coefficients
Substitute yp
(x) and its derivatives in the differential equation
and evaluate symbolically.
To make it easy to compare similar terms, we use the
command "collect" on the variable x. This
will rearrange the terms as a polynomial in x. This
step will help you in the computer project.
Equate similar terms to find the linear system involving
the undetermined coefficients. This step has to be
done manually.
Place the equations of the system in a vector and use
the "solve" command to find the coefficients.
Define the coefficient as solved for in the previous
step.
f5. Write the particular solution after finding the
coefficients
Redefine the particular solution and evaluate symbolically
to display it.
Note: This redefinition is required by Mathcad so that
it can substitute the values of the coefficients.
f6. Write the general solution of the nonhomogeneous
equation
Define the general solution y(x) as the sum of the complementary
solution and the particular solution and evaluate symbolically
to display the result.
g) Use the following steps to find a particular
solution of the nonhomogeneous equation satisfying
the given initial conditions:
g1. Apply the first initial condition on the general
solution in part f6.
Evaluate y(x) at the initial point and set it equal
to the initial value, then evaluate symbolically to
get the first equation of the linear system involving
the arbitrary constants.
g2. Compute the first derivative of the general solution
in part f6 and apply the second initial condition
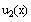 and compute symbolically.
and compute symbolically.