g7) Substitute the above values in the general solution
of the nonhomogeneous equation to obtain the particular
solution
2. Given that
is the complementary solution of the differential equation
find a particular solution of the equation using the
method of variation of parameters.
3. Given that
1, -1, -1, 1+ i, 1 + i are the roots of the characteristic
polynomial of a linear homogenous differential equation
with real constant coefficients L y(x) = 0
a) Find the operator L using the
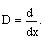
notation.
Note:
You may leave L in a factored form but make sure that
it does not involve complex numbers.
b) Write the general solution of the differential
equation.
4. Given the linear
system
a ) Find a basis for the solution space of the system
b) Justify (without computation) that the basis
vectors are linearly independent.
c) What is the dimension of the solution space?
Why?
5.
Let V be the set of all vectors in
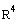
such that: if v =
e
V, then
and
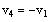
. Show that V is a subspace of
.
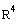
6.
Justify without solving that the vectors
7.
Answer the following questions with (T)rue or (F)alse.
Penalty: An incorrect answer will cancel a correct
answer.
________ In an n-dimensional vector space V, a vector
in V can be written in one and only one way as a linear
combination of a set of n linearly independent vectors
in V.
________ The dimension of a vector space V is the number
of elements in V.
________ In an n-dimensional vector space, a set of
n-1 vectors must be linearly dependent.
________ Every subspace of a vector space contains the
zero vector.
________ If a set S spans the vector space V, then S
contains a bases for V.
________ Any set of vectors that spans a vector space
V must be linearly independent.
________ Any lineally independent set of vectors in
Rn forms a basis for Rn
________ If a set S in a vector space V is linearly
independent, then it contains a basis for V.
________ The principle of superposition states that
if x and y are two solutions to a homogeneous system,
then any linear combination of x and y is also a solution
to the system.
________
The solution space of a homogeneous linear system of
3 equations in 4 unknowns is a subspace of R4
Answer all questions, show
all your work!
1.
Execute the following steps to find a solution to the
differential equation
satisfying the initial conditions
a) Write the associated homogeneous equation
b) Find the roots of the characteristic equation
c) Write the complementary solution
d) Show that the two solutions of the homogeneous
equation are linearly independent. Justify your answer
e) Give the interval over which the two solutions
of the homogeneous equation are linearly independent
f) Use following steps to find the general solution
of the nonhomogeneous equation using the method of
undetermined coefficients:
f1. Write the unmodified form of the particular solution
f2. Write the modified form of the particular solution
yp
f3. Compute the first and second derivative of yp
f4. Substitute yp
and its derivatives in the nonhomogeneous equation,
simplify, and equate similar
terms to determine
the coefficients
f5. Write the particular solution after finding the
coefficients
f6. Write the general solution of the nonhomogeneous
equation
g) Use the following steps to find a particular
solution of the nonhomogeneous equation satisfying
the given initial conditions:
g1. Apply the first initial condition on the general
solution in part f6.
g2. Compute the first derivative of the general solution
in part f6 and apply the second initial condition
g3. Write the linear system obtained in parts (g1) and
(g2) as a matrix equation A c = b
g4) Form the augmented matrix of the system above
g5) Compute the reduced row echelon form of the augmented
matrix to solve the system
g6) Give the values of the constants c1 and c2 found
above
