we get the first basis vector
we get the second basis vector
5.
Given the initial value problem y'' + 4 y = 2 cos(2
x), y(0) =
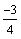
, y'(0) = 4
a) Find the complementary solution
Mathcad Note
: The variables x and c1
and c2
have been assigned values before. To reset their assignments,
we use the commands:
(Find the roots of the char. eqn)
b) Use the method of undetermined coefficients to find
a particular solution
Mathcad Note
: The variable A has been used to define the matrix
A. To use it as a constant, we have to reset its value
with the command:
(Unmodified form of the particular soln)
(Form of the partic. soln. (since the complex root ±2i
has multiplicity 1 we multiply by x)
(Multip row 2 by - 3 /7 and add to row 1)
3. Show whether
or not W = {
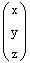
| z = 2 x +3 y } is a subspace of
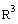
.
If u is an element in W, then the third component of
u is 2 times the first component + 3 times the third
component.
Let u and v be elements in W
==>(by definition of vectors in W)
Thus, u + v satisfies the definition of elements in
W ==> W is closed under addition.
Let c be any scalar, then
Again, a scalar multiple of u satisfies the definition
of elements in W ==> W is closed under scalar multiplication.
Therefore, W is a subspace of R3
.
4.
Find a basis for the solution space of the system
Mathcad is used to solve system
Thus, the solution has two free variables x3 and x4
(Assign the result to c2
)
(This is the particular soln satisfying the initial
conditions
(Check if the particular satisfies the initial condition.)
(Compute the deriv of the particular soln.)
(Check if the deriv of the particular soln satisfies
the initial condition.)
(Check the partic. soln into the diff. eqn)
6.
If -1 is a root of the characteristic equation of
the differential equation
find the form of the particular solution.
Unmodified particular solution:
Modified particular solution:
Substitute in the diff. eqn.
Equate similar terms and solve for A, and B (the results
are assigned to A and B)
Thus, with the above values of A and B, the particular
solution
c) Find the general solution.
d) Find a particular solution satisfying the initial
conditions
(Evaluate the solution at x = 0 and set it equal to
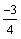
)
(Assign the result to c1
)
(Compute the deriv. of the soln)
(Evaluate the deriv at x = 0 and set it equal to 4)
We can now display the solution as
Another way to solve the system is to compute the reduce
row echelon form of the augmented matrix [ A | b ].
(Define the augmented matrix and name it Ab)
(Use Mathcad rref command to compute the reduced row
echelon form of the augmented matrix.
The solution can be read from the last column of the
reduced matrix)
A third way to solve the system is to use the solve
command.
Define the equations as elements of a 3 x 1 vector and
use Mathcad solve
command.
b) Find the inverse of the coefficient matrix using
the adjoint method.
Note:
Mathcad commands are used to solve some of the problems
in this exam.
(Set the initial subscription index to 1)
1. Given the linear
system
a) Use Cramer's Rule to solve the system
(Define the coefficient matrix)
(Compute the determinant of A)
(Construct the numerator by replacing the first column
of A by the vector b)
(Display the numerator defined above)
(compute the determinant)
The above process is repeated for x2
and x3.
for
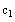
and
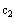
.
Augment the vectors u, v and w
Compute the rref of the aug. matrix
(Define row functions R1(z) and R2(z) to do row operations
on the augmented matrix z)
(Multip row 1 by -5 and add to row 2)
Thus, the cofactor matrix is
and the adjoint matrix is the transpose of the cofactor
matrix
Thus, the inverse of the matrix A is obtained by the
formula
We can check our answer my multiplying A time its inverse
to get the identity matrix
c) Check your answer in part (a) by solving the system
using the inverse method.
2. Express the
vector
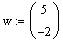
as a linear combination of the vectors
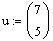
and
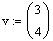
To write the vector w as a linear combination of u and
v, we need to solve the linear system