Combine the logs using the property:

Therefore,

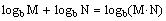
Expand and rewrite as zero equation.

Solver for x

Upon substituting the solutions into the original equation, we find that -7 could not be a solution.

Thue, the solution set is S = {0}

Mathcad check:

c)

Solution:

Use the property

Apply the arrow rule: Solve for the argument by raising the base to whatever is on the other side. The direction of the inequality is kept (not reversed) since the base is greater than one.

Solve for x

Mathcad check:

Mathcad is unable to solve the double-sided inequality.

It can do one side,

then the other. The solution will be the intersection of the two intervals.

b)

Solution:

To avoid division, move the negative term to the other side.

==>

Therefore,

Mathcad check:

6. Write as a single logarithm

Solution:

Mathcad check:

Answer the following questions with T (rue) or F (alse). Note: An incorrect answer will cancel a correct answer.

___T___ a) .

___T___ b) .

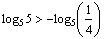
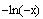
___T___ c) is an increasing function.

___T___ d) The function has no x-intercept and and y-intercept equal to zero.

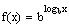
___F___ e) The graph of is the same as the graph of g(x) = x.

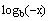
___F___ f) The function is undefined for all x.

___F___ g) .

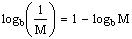
___T___ h) Life does not always give you a second chance.

==>

or

==>

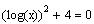
has no real solution

Mathcad check:

Mathcad is returning the complex solution as well.

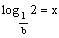
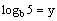
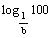
4. If and , express in terms of x and y.

Solution:

5. Find the value of

Solution:

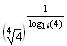
b)

Solution:

==>

and

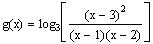
Set the factors to zero and solve for x

So, we have only three open intervals:

and

Choose a point in one of the intervals and substitute in the inequality to check for sign.

Math 002-043-A. Farhat

Major Quiz 1

July 12, 2005

Name:

Student ID:

Section #.:

List #.:

Answer all questions. Show all your work

Cheating in punishable by an F-grade for the course.

1. Find the domain of the functions:

a)

Solution:

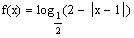
Set the argument greater than zero and solve for x

==>

==>

==>

Mathcad check:

Shift up by 2 units

Figure 1

b) Find the range of f(x) ( do not use the graph)

Solution:

Start with the range of the exponential function

Multiply by -1 and reverse the inequality

Add 2 to all sides (- will not be affected).

Rewrite in standard form (small numbers to the left) by reading the previous inequality from the right.

3. Solve for x

a)

Solution:

Choose the point 0 in the first interval and substitute in the inequality.

Therefore, the point satisfies the inequality and ever point in that interval in a solution. Now we take every other interval (take one, leave one). Thus, we skip the interval (1, 2) and take the interval . However, the point x = 3 can not be taken because it is not part of the solution due to the strict inequality.

Mathcad check:

2. Let

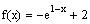
a) Sketch the graph of

Solution:

As discussed in class, it better to do the shifting then the reflection in the x-direction, and the

S

reflection then the shifting in the y-direction ( Remember the rule: S __ | )

Figure 1 illustrates the steps of graphing the function starting with the graph of .

Basic graph

Shift left by one unit

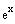
Reflect about the y-axis

(Replacing x by -x)

Reflect about the x-axis

(Replacing y by -y)