where k is the quotient of the division
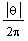
Since the angle A is negative, the coterminal c is obtained
by the formula
See lecture notes: "Computing the Coterminal Angle."
a)

1. Find the coterminal angle of the angles
Note: Mathcad uses the function
log(x,b) for logbx
Note:

==> x = 3 or x = -3. However, -3 is rejected
since the base has to be greater than one.
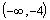 È
È 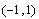 È (1, ¥)
È (1, ¥)
So, the interval
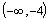
is a good one, i.e., every point in this interval will
satisfy the inequality. Next, we choose every other
interval. Thus, we leave the interval (-4, -1) and
take the interval
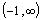
with the exclusion of the point 1.
The two intervals surrounding the point 1 is considered
as one region because it is coming from a factor raised
to an even power. So, we basically have three intervals:
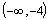 , (-4, -1)
and
, (-4, -1)
and 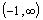 (excluding
the point 1)
(excluding
the point 1)
Choose a point in any interval, say x = -100 and substitute
into the inequality to check for the sign:
So,
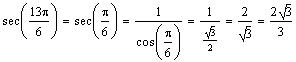
b)

But
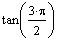
is not defined because
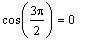
Therefore, the coterminal angle is
First, we find the coterminal angle
Where k is the quotient of the division
Since the angle b in positive and is in degrees, the
coterminal angle c is obtained by the formula
Note:
This method works well provided that non of the factors
is raised to an even power. If this is the case, then
the two intervals surrounding the zero of that factor
is considered as one region because there will not
be a change of sign around this point.
(-1, 0)
È
(1,
 )
)
Thus, the point x = 100 satisfies the inequality and
every point in that interval will also satisfy the
inequality. Now, every other region will also satisfy
the inequality. Hence, the domain is:
Non of the points is part of the domain since we do
not have equality.
Pick a region and choose any value in that region, say
x = 100, which lies in the interval (1,
 ).
).
Substitute x = 100 into the inequality to check for
the sign. Here we have,
Therefore, the roots (zeros) are: 0, 1, and -1. These
points divide the real line into four intervals as
shown below:
Factor and set greater than 0
The domain is obtained by setting the argument greater
than zero and solving the inequality for x
Find the domain of the function

Select the points to plot
Sketch the graph of the function
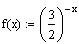
Sketch the graph of the function
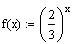
Therefore , the solution is x = -5
Submitting x = -5 into the original equation, we find
that it satisfies the equation. But x = -10 will result
in a negative argument for the log.