Graph of the basic function:

Shift the graph of the basic function up by two units
Check your answer by substituting x = 0 to verify that
the graph passes by the point (0, 3)
b)
find the domain, range and asysmptotes (if any) of
f(x)
add 2 to all sides of the inequality
Horizontal asymptote: As x --> -
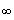
, y --> 2
Thus, the line y = 2 is a horizontal asymptote
c) find the inverse
of f(x)
Let
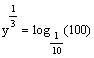
. Find the value of y
Raise both side to power 3
6. Let
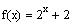
a) sketch the
graph of f(x)
Take the antilog of all sides.
Keep the direction of the inequalities since
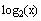
is an increasing function
Multiply by -1 and reverse the direction of inequality
Take the antilog and reverse the direction of the inequality
since
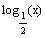
is a decreasing function.
Take log base 2 of both sides
7. Solve for
x

Isolate
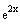
Take natural log of both sides
So, the graph of
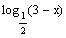
should pass by the point (2,0).
b)
find the domain, range and asysmptotes (if any) of
f(x)
Thus, the line x = 3 is a vertical asymptote.
c) find the inverse
of f(x)
Answer all questions. Show all your work
Let

a) sketch the
graph of f(x)
Graph of the basic function:
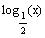
As discussed in class: When there is a combination of
shifting and reflection about the y axis, we do the
shifting first.
Shift the graph of
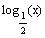
to the left by 3 units to get the graph of
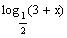
Reflect the graph of
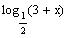
about the y axis to get the graph of
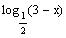
You may check your answer by substituting x = 2:
Upon checking the answers in the original equation,
we find that x = - 23/3 is not a solution. Thus the
solution set is { 3 }.
Write as a single logarithm and simplify your answer:
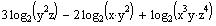
(Insert the coefficients inside the log as exponents)
Find the solution set of the function
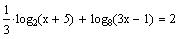
Multiply the equation by 3
