Solution:

Find the equation represented by the graph shown below.

------------------------------------

Graph of the parabola.

Directrix:

Focus:

Vertex:

Therfore,

==>

Rewrite the eqn. to the standard form

Solution:

031-T2-15

031-T2-14

Eqn of the left half

or

Eqn of the right half.

Thus,

Solve for x to find the eqns of the right and left sides of the ellipse.

==>

Eqn of the ellipse

This is the graph of the right half of a standard ellipse.

==>

Choose

Solve for

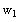
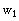
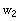
We can only solve for either or in terms of the other.

Compute the dot product and set it to zero.

Mathcad thing

u and v are orthogonal

then

Let

Solution:

Find a nonzero vector that is perpendicular ot the vector u = < -2, 7>

Section 7.3

Find the vertex, focus and the directrix of the parabola .

Section 8.1

031-T2-17

031-T2-13

031-T2-12

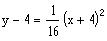
For the vectors u, v and w shown in the figure, which one of the following relations is TRUE?

--------------------------------------------

Thus,

You may choose any real number for

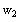
To find the point of intersection:

Therefore, the intersection will be in the Quadrant I only.

The fact that y is under the square root ==> that y must be positive.

The fact that x is equal to the squre root of something ==> x must be positive.

Solution:

031-T2-16

Therefore, the equation of the ellipse is:

==>

==>

or

==>

==>

or

==>

==>

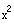
Substitute in the second equation

==>

and

Foci:

Center:

Complete the squares

Solution:

031-T2-9

Section 8.2

==>

and

Center:

Midpoint formula

Form of the ellipse read from the given foci

Solution:

031-T2-11

031-T2-10

==>

Which one of the following is FALSE?

Section 6.6

031-T2-19

Section 6.5

031-T2-5

Section 6.4

or

==>

or

Solution:

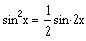
Find the number of solutions of the equation over the interval [0, 3p /2)

---------------------------------------

------------------------------------------------

Section 6.3

031-T2-2

033-T2-1

Section 6.2

Section 6.1

A. M. Farhat

Old Exams Problems

Math002

031-T2-4

031-T2-6

031-T2-7

031-T2-22

031-T2-3

Ans. 1

Ans:

------------------------------------

and

==>

==>

or

Rewrite the eqn

==>

The zeros of f(x) are obtained by setting f(x) = 0 and solving for x.

Solution:

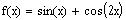
Find the zeros of the function in the interval [0, 2p)

031-T2-22

==>

Recall:

Solution:

---------------------------------------

Solve for x.

==>

k is an integer.

==>

Solution:

Find the set of solutions of the equation sin3x = 1.

Find all the solutions of the equation ,

----------------------------------

Mathcad check:

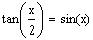
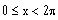
Expand the cosine of the difference

Apply cosine to both sides.

Rewrite the eqn.

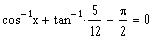
Solve the equation for x.

-------------------------------------

The number of solutions is 4.

or

==>

--------------------------------

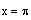
Note: is not a solution since is not defined.

or

==>

or

==>

==>

Divide by sin(x) and consider that sin(x) =0 may include solutions.

==>

==>

Solution: