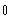e)
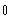
d)
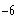
c)
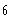
b)
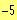
a)
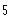
then
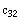
, the third row and second column of C equals
10.2.1. (001-Final-5
$10.2)
Solve the system for a, b and c.
Note: We only need to compute the first row of the product
and equate it to the first row of the identity matrix.
e)

d)
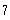
c)
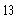
b)
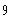
a)
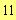
The matrix M and its inverse are given by
10.3.1 (001-Final-18
$10.3)

is obtained by multiplying the 3rd row of A by the second
column of B.
Substitute the given point into the equation of the
parabola to get a system of 3 equations in 3 unknowns.
e)

d)
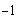
c)
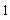
b)

a)
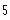
10.1.6 (002-Final-17
$10.1)
e)
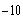
d)
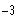
c)

b)
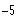
a)

10.4.2 (002-Final-18
$10.4)
e)
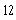
e)
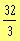
d)
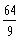
c)
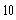
b)
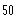
a)
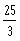
10.4.3 (002-Final-25
$10.4)
d)
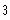
c)
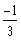
b)
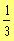
a)

10.3.2 002-Final-16
$10.3
d)
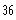
c)
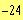
b)

a)
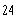
What is the value of the following determinant?
10.4.1 (001-Final-8
$10.4)
Compute the reduce row echelon form of the augmented
matrix to find
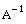
Augment the matrix A with the identity matrix
e)
Use the rref command to compute the reduced row echelon
form.
This is the reduced row echelon form.
This is the echelon form. We can now use back substitution
to find x, y and z.
However, it is better to complete the reduction to find
the reduced row echelon form and then read the solution
from the reduce matrix as shown below.
e)
d)
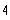
c)
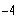
b)
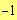
a)
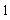
10.1.3 (001-Final-26
$10.1)

==>
e) The system is consistent for c > 0.
d) The system is inconsistent for all values of c.
c) The system can be made consistent for a suitable
choice of c.
b) The system is consistent for all
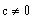
, with exactly one solution.
a) The system is consistent if c = 0, with infinitely
many solutions.
Which one of the following statements is TRUE about
the linear system of equations which has the augmented
matrix
10.1.1 (001-Final-12
$10.1)
Solution of Old Exams Problems
Chapter
10
e)

d)
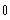
c)
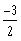
b)
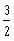
a)
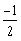
10.1.2 (001-Final-22
$10.1)
The system has a leading entry in the last column ==>
the system has no solution regardless of the choice
of c.
d)
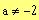
and
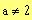
c)
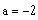
and
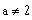
b)
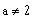
a)
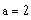
and

10.1.5 (002-Final-15
$10.1)
Case II (Infinite number of solutions)
Reduce the augmented matrix.
e)
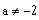
Augmented matrix of the new system
10.1.4 (002-Final-7
$10.2 )