The fact that x is equal to the square root of something
==> x must be positive.
The fact that y is under the square root ==> that
y must be positive.
Therefore, the intersection will be in the Quadrant
I only.
To find the point of intersection:
Substitute
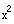
in the second equation
Form of the ellipse read from the given foci
Therefore, the equation of the ellipse is:
Find b in terms of a using the given slope.
Substitute the center and b.
Substitute the given point.
Form of the hyperbola. Transverse axis parallel to the
x-axis ==> x term is positive.
This is the graph of the right half of a standard ellipse.
Solve for x to find the eqns of the right and left sides
of the ellipse.
Solution of Old Exam Problems
Chapter
8
Find the vertex, focus and the directrix of the parabola
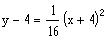
.
Rewrite the eqn. in the standard form
Find the equation represented by the graph shown below.
b)
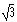
d)
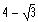
e)
