Take the cosine of both side
d) A solution x
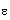
(0, 1]
c) A solution x

a) Exactly one solution which is a negative integer
The number of solutions of the equation
Therefore, equation (1) becomes
Expand the cosine of the difference
Apply cosine to both sides.
e)
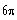
d)
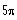
c)
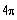
b)

a)
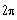
The sum of all the solutions of the equation
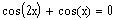
in the interval
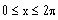
is equal to
The zeros of f(x) are obtained by setting f(x) = 0 and
solving for x.
Find the zeros of the function
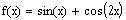
in the interval [0, 2
p)
Note:
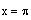
is not a solution since
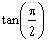
is not defined.
Find the set of solutions of the equation sin3x = 1.
Find the number of solutions of the equation
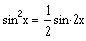
over the interval [0, 3
p
/2)
If we substitute x = -1 and x =
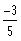
in equation (2), we find that only x = -1 satisfies
the equation.
Divide by sin(x) and consider that sin(x) =0 may include
solutions.
Find all the solutions of the equation
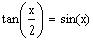
,
The number of solutions is 4.
c)

b)
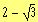
a)
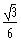
The cosine is positive and the sine is negative in quadrant
IV. Thus from the graph
e)
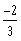
d)
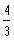
c)
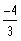
b)

a)
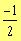
where the choice of (+) or (-) depends on the quadrant
in which the half-angle
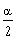
terminates.
e)
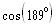
d)
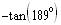
c)
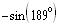
b)
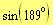
a)

Rationalize the denominator
e)

d)
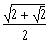
c)
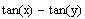
b)
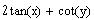
a)
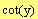
e)
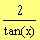
d)
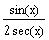
c)

b)

a)
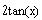
The expression
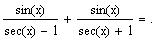
Solution of Old Exams Problems
Chapter
6
Therefore, by substituting (1) and (2) we have
Working on the second term.
Working on the second term.
e)
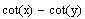
d)
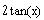
The sine and cosine of
a
are
negative ==> a
is in quadrant III. From the values of the sine and
cosine we compute the reference angle of a. The reference angle is
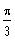 .
.
Therefore,
e) k = 2,
a
=
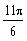
d) k = 2,
a
=
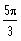
c) k = 2,
a
=
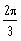
b) k = 2,
a
=

a) k = 2,
a
=
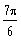
When writing
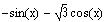 in the form
of
in the form
of 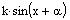 ,
, 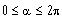
,
then
Solve the equation
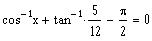
for x.
if
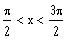
(Only if x is in the range of arcsine)
if
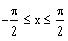
.
e)

d)

c)
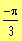
b)
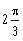
a)
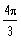
The maximum value of the function
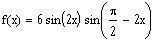
is:
e)
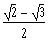
d)
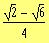
c)
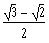
b)
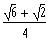
a)
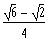
The exact value of
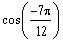
is:
Graph of
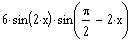
The maximum values will occur when sin (4x) = 1
Find all the x values at which the function has maximum
values
Thus, the maximum value of f(x) is 3.
Use the double angel identity of the sine
Use the cofunction identity.