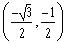a)
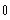
b)
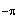
c)

d)
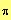
e)
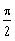
The asymptotes of the tangent function y = tan
q are at the zeros
of cos(
q)
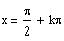
Therefore, the asymptotes are obtained when
Create a table to compute x for different values of
k
Consider that the graph represents a sine function
a sin (bx + c) shifted to the left.
Read the amplitude from the graph.
Read the phase shift from the graph
If x = a and y = b are the 2 asymptotes of
Multiply by
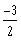
. This will cause the inequalities to reverse directions
Thus, the range in interval notation is b) R = (-¥ , -1/2] U [5/2,
¥)
Find the smallest positive angle coterminal
with the angle
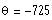
.
Verify the identity
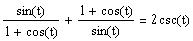
Find the values of x and y such that
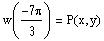
A wheel is rotating at 100 revolutions per minute, find
the angular speed in radians per second.
Sketch the graph of
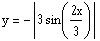
If
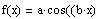
, b > 0, period = 6 and f(3) = 4, find

The first and the last rows are not inside the given
interval.
So, in the interval
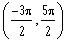
, the asymptotes are at
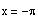
and
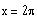
Graph of
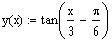
The range and the period of

are:
a) R = (-¥
, -1/2] U [5/2, ¥)
, P = p/3
b) R = (-¥
, -1/2] U [5/2, ¥
), P = - p/3
c) R = (-¥
, -1/2] U [5/2, ¥
), P = 2p/3
d) R = (-¥
, -3/2] U [3/2, ¥
), P = 2p/3
e) R = (-¥
, -5/2] U [1/2, ¥
), P = 2p/3
The period =
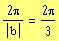
a)
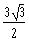
b)

c)
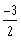
d)

e)
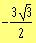
The top of a radio antenna is 100 m high from the ground.
A wire 200 m long is attached to the top from the ground.
What is the angle the wire makes with the ground.
a)
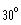
b)
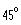
c)
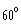
d)
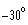
5.2.3 (002-Final-2
$5.2 )
a)

b)
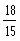
Solution of Old Exams Problems
Chapter 5
5.1.1 Covert the
angle
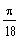
radians to revolutions
Multiply by the conversion unity

A wheel of a truck has a radius 1.6 feet.
a) How far
will the truck move if the wheel turns through 40o
?
b) If the wheel
is rotating at
the rate of 6 revolutions
per second, find the speed
of the truck in feet per second.
The value of the expression
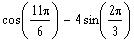
is equal to:
Since the angle is negative, we find the coterminal
angle using equation:
coterminal angle =
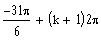
See lecture notes: Computing the coterminal angle.
To find k, divide
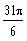
over 2
p
coterminal angle =
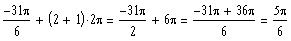
The adjacent graph represents, over one period, the
following function:
a)
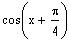
b)
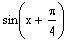
c)

d)
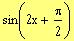
e)
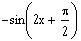
c)
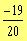
d)
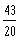
e)
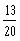
Choose a negative
value for x and compute y.
The rectangular coordinates of the point

on the unit circle is:
a)
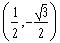
b)
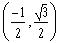
c)

d)
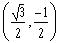
e)