The special 30-60 triangle with hypotenuse 1 can be
remembered as a triangle having a "short"
side equals

, and a "long" side equals
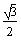
.
This triangle can be inscribed inside the unit circle
and used to find the values of the cosine and the sine
functions (and consequently the rest of the trigonometric
functions) for any multiple of 30-degree angles. Figure
2 illustrates the division of the unit circle in terms
of multiples of 30 degrees (
p
/6 radians). It helps to remember the quadrantal angles
as 0, 90, 180, 270, and 360 degrees (0,
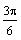
,
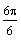
,
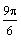
, and

radians).