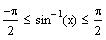4.

____________O___________

Again, Mathcad will only give answers that lie in the range of the inverse sine function, i. e.,

Check using Mathcad

==>

==>

Divide by 2

or

==>

Use unit circle

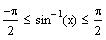
Take sin(2x) as a common factor

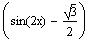
Take as a common factor

Thus,

or

Use the zero product property

or

==>

or

Solve for t

or

Substitute cos(x) for t

==>

or

==>

Given

To find the other angle (in Quadrant IV) whose cosine is 1/3, we subtract 70.5 from 360:

Given that cos-1(1/3) = 70.5o , solve for x in the interval

Solution:

Let

Substitute t for cos(x)

==>

Factor

or

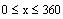
(Which property did we use?)

or

The solutions are:

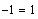
If we substitute x = 180o in the original equation, we get . Similarly for the value

x = 270o. Thus, x = 180o and x = 270o are not solutions.

However, because we squared both sides in the process of the solution, one has to be careful about introducing "extraneous" solutions (solutions that will not satisfy the original equation).

or

or

or

Use zero product property

or

Divide by 2

Math 002-041

Major Quiz 8 Solution

Nov. 29, 2004

Answer all questions. Show all your work

Solve the following problems for x:

1.

Solution:

Square both sides

Expand

Use the identity

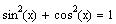
Using the fact that the sine function is odd

The sine function is negative in Quadrant III and IV. Using the method of the unit circle (see Lecture Notes web page), we have

or

Check using Mathcad:

Remark

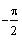
Mathcad returned only one value because it used the inverse sine function (sin-1 ). Recall that the range of sin-1(x) is between and .

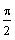
_____________O_____________

3.

Solution:

Group to take common factors

or

Remark

Mathcad can be used to check your answer using the "solve" command as follows:

The solution is given in radians which is the same as the one we obtained in degrees.

____________O_____________

2.

Solution:

Using

Where

and