Multiply by 13

==>

Rewrite to place the radical on one side before squaring the two sides of the equation.

Check using Mathcad

4. Find the domain and range of

Solution:

Domain:

==>

Range:

Use the fact that

(see Figure 4)

==>

==>

and

(see Figure 5)

Substitute in (1)

Figure 4

Figure 5

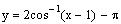
We now equation the expression above to 1 and solve for x

==>

a)

False

Let x = 1

then

and

undefined

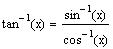
b)

False

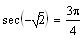
The secant of a negative number less than minus one is negative.

c)

True

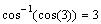
Because 3 is in the domain of cos and in the range of cos-1.

d)

False

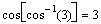
Because 3 is not in the domain of cos-1.

e)

False

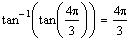
Because 4p / 3 is in the domain of tan but not in the range of tan-1 .

recall:

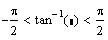
Remark:

The general rule for deciding on the possible values of x in a composite function of the form:

outside_function(inside_function(x))

is: x must be in the domain of inside_function and in the range of outside_function.

Multiply the inequality by 2.

Subtract p from all sides.

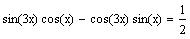
5. Solve the equation , where

Solution:

Thus,

==>

or

==>

or

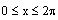
6. Answer with true or false

==>

==>

(see Figure 2)

Please ignore

the guys above.

They are used

to draw the

graphs.

Note:

The coordinates of the graphs are not scaled equally.

13

5

12

3

4

5

Figure 1

Figure 2

Thus,

Math 002-041

Solutions to Cal Problems 6.5 - 6.6

A. Farhat

1. Find the exact value of .

Solution:

Let

and

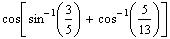
This substitution transforms the question to finding the value of .

5

==>

==>

(see Figure 1)

Thus,

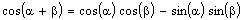
3. Solve the equation .

Solution:

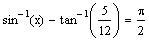
Take sine of both sides and evaluate .

Let

and

Thus, we need to find

(1)

==>

==>

Check using Mathcad:

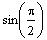
This says that Mathcad is unable to find the exact value.

This says that Mathcad can find the approximate value.

2. Verify the identity .

Solution:

LHS = Left Hand Side

Let

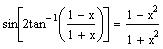
This substitution transforms the problem to that of finding

sin(2 a) = 2 sin(a) cos(a).

==>

==> (See Figure 3)

and

Figure 3