Note that to complete the square for x we added

not
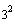
Here we have an ellipse with major axis parallel to
the y axis since the bigger denominator is under the
y term.
39+.
Find the equation of the ellipse with center (3, 4),
major axis of length 4, foci (3, 3) and (3, 5)
The bigger number (25) is under the
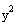
. This tell us that the major axis of the ellipse is
parallel to the y-axis (a vertical ellipse).
23.
Find the vertices and foci of the ellipse
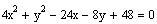
We need to complete the square for both variable.
Regroup and move the constant to the other side.
Pull out the coefficient of
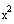
and leave room for completing the square.
Multiply both sides by
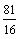
This is the equation of an ellipse with major axis parallel
to the y axis.
We now know that the given equation is the equation
of half an ellipse. Which half? From the equation we
can see that all the x values will be greater than
-5. Thus, the equation represents the right side of
the ellipse with the above properties.
major axis of length 4 ==>
49.
Find the equation of the ellipse with eccentricity
2/5, foci at (-1, 3) and (3, 3).
The center of the ellipse will be at the middle point
between the two foci.
c is half the distance between the two foci. ==>
Substitute c in equation (1), we get
Thus, the equation of the ellipse is
E1. Sketch the
graph of
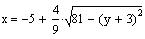
Rearrange the equation to make the quadratic variable
on one side and the other variable on the other side.
Take 2 as a common factor and leave room for completing
the square.
Factor out the coefficient of y
This is a equation of a parabola that opens upward,
with:
Solution of Homework Problems Minus One
Chapter
8
10+.
Find the vertex, focus and directrix of the parabola
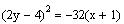
The equation is not in the standard form
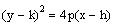
. Thus, we must first right it in the standard form.
Take 2 as a common factor
Use the property
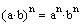
This is the standard form of a parabola that opens to
the left.
21+.
Find the vertex, focus and directrix of the parabola
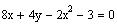
Multiply the equation by -1 to make the squared term
positive and rearrange the equation
36+.
The LNB (in instrument to collect satellite signals)
is to be placed at the focus of a
paraboloid dish. If the dish has diameter
120 cm and a depth of 40 cm, how far from the vertex
of the paraboloid should the LNB be place.
This problem was discussed in class.
E1. Sketch the
graph of
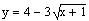
This is the equation of a parabola that opens to the
left.
Thus, the given equation represents half a parabola.
The question is: "Is it the upper half or the
lower half?" A closer look at the given equation
tells us that the y values will always be greater than
2. This helps us choose the upper half of the parabola.
The graph below illustrates the two halves of the parabola.
1.
Find the vertices and foci of the ellipse
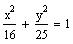
31. Find the equation
in standard form
of the parabola with focus (3, -3) and directrix y =
-5 .
The equation of the directrix y = constant ==> the
parabola opens either upward or downward. Moreover,
the directrix is below the focus (by comparing the
values -5 and -3) tells us that the parabola opens
upward.
Therefore, the equation of the parabola will have the
form
Now, the point on the directrix directly below the focus
will have coordinates (3, -5). We can now use the midpoint
formula to find the vertex, which is in the middle
between the point (3, -5) and the focus (3, -3)
To find p we have to choices:
1) Compute the distance between the vertex and the focus
2) Compute half the distance between the focus and the
point (3, -5) on the directrix.
Thus, the equation of the parabola is given by:
33.
Find the equation in standard form of the parabola
that has vertex (-4 , 1), has its axis of symmetry
parallel to the y-axis, and passes through
the point (-2, 2)
A parabola with axis of symmetry parallel to the y-axis
has the form:
The parabola passes through the point (-2, 2) ==>
the point satisfies the equation of the parabola.
Substitute the point in the equation to compute p