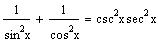So, now we look for the angle in quadrant I or quadrant
II whose cosine is
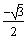
. That angle is
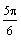
(see Figure 2)
Using the unit circle, we have (see Figure 1)
We know that
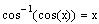
but only if x is in the range of

. That is, only if
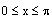
. Therefore, we can not use this property (this is not
to say that we can not find the value).
31+. Find the
exact value of
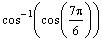
So, we look for the angle in the quadrant I or quadrant
IV whose sine is
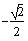
. The angle is
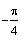
Recall that if x is in the domain of

, that is, if
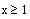
or
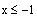
then
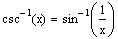
11. Find the exact
value of
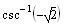
The logical choice should be the second one because
cos (
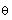
) is readily available by applying the cosine to both
sides of equation (1).
This means that we are looking for cos (2q). To find cos
(2q
), we have three choices:
50+. Find the
exact value of
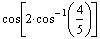
Here, it is better to start with the right-hand side.
33. Verify the
identity
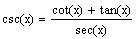
27+. Verify the
identity
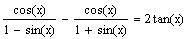
Multiply and divide by
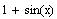
21. Verify the
identity

13. Verify the
identity
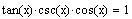
Most of the problems are selected from the textbook.
They are usually the ones that precede a homework problem.
The intention is to give the student a close example
to help him solve the homework assignment. If the homework
problem and the one preceding it are not similar, another
problem is created and a (+) sign is added to the number
of the problem.
Solution of Homework Problems Minus One
Chapter
6
take
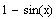
as a common factor
take cos(x) as a common factor
take 2 as a common factor
Using the expansion
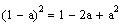
where
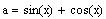
Start with the left-hand side and regroup as follows:
63+. Verify the
identity
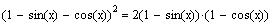
41. Verify the
identity