DO LOOPS
Problem#1
A leap year is any year that is a
multiple of 400 or that is a multiple of 4 but not a multiple of 100. Write a
logical function ISLEAP which determines whether a year is leap or not. Write a
main program which uses the logical function to print all leap years in the
range 1950 to 1999.
Your output should be:
THE
LEAP YEARS BETWEEN 1950 AND 1999 ARE:
1952
1956
1960
1964
1968
1972
1976
1980
1984
1988
1992
1996
Problem#2
Write a program that reads three
integer values into the variables M,
K and J such that the value of M is less
than or equal to the value of K. The program should then pass the three
values to a function that computes and returns the number of values between M
and K that are divisible by J. The value returned to the main program should be
printed.
Problem#3
A prime number is an integer
greater than 1 that has no divisors other than 1 and itself (e.g., 2, 3, 7).
Write a program which will print all the divisors of a positive integer N other than 1 and itself. If
there are no such divisors, the program should print out the message: XX IS A
PRIME NUMBER where XX is the value of N.
HINT: The divisor of a number,
except for itself, cannot be more than the square root of that number.
Use the data: 195
Your output should be:
LIST OF DIVISORS OF 195 EXCEPT 1
AND 195 :
3
5
13
Problem#4
Write a program which prompts for
and reads a positive integer N. The program then reads N real values. Each time
a real value X greater than 0.0 is read the program calls a REAL function LENX
which returns the ln of X. The program then prints X and its ln. If X is less
than or equal to zero the program prints X and the message UNDEFINED LEN.
The function LENX computes the ln
of X by summing the first 100 terms of the infinite series:
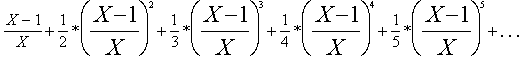
Use the following data:
6
2.0
0.0
5.0
-3.0
8.5
30.4
Your output should be:
X LN(X)
2.000000 6.931473E-01
0.000000E+00 UNDIFENED
LEN
5.000000 1.609438
-3.000000 UNDEFINED
LEN
8.500000 2.140066
30.400000 3.406164
Problem#5
Write a program that finds an approximation for p using
the first 10000 terms of the following infinite series:
p2 =
6 / 12 + 6 / 22 + 6 / 32 +
. . .
Your output should be:
PI = 3.141363
Problem#6
Write a program that finds an approximation for p
using the first 10000 terms of the following infinite series:
p
= 4 - 4 / 3
+ 4 / 5 - 4 / 7
+ 4 / 9 - . . .
Your output should be:
PI = 3.141498
Problem#7
Write a program which uses a do-loop to find the sum of the
following series:
1 + (1 * 2) +
(1 * 2 * 3) + (1 * 2 * 3 * 4) + . . .
+ (1 * 2 * 3 * . . .
* 20)
Your output should be:
SUM = 2.561327E+18
Problem#8
Write a program which finds the sum of the following series:
___ ______ __________ ___________________
Ö
1
+ ? 1
+ 2 + ? 1 +
2 + 3 +
. . .
+ ? 1
+ 2 +
. . .
+ 100
Your output should be:
SUM = 3605.837000
Problem#9
Write a program
which calculates and prints the sum of the first 300 terms of the infinite
series:
2 5 8 11
--- + --- + --- +
---- + . . .
2 6 10 14
Your output should be:
SUM =
225.958400
Problem#10
Write a program
which calculates and prints the sum of the first 200 terms of the infinite
series:
9 13 17 21
--- + ---- + ---- + ---- + . . .
6 9 12
15
Your output should be:
SUM =
268.294300
Problem#11
Write a program
which calculates and prints the sum of the first 100 terms of the infinite
series:
1 3 5
7
--- + --- + --- +
--- + . . .
2 4 6
8
Your output should be:
SUM =
97.406300
Problem#12
Write a program which calculates and prints the sum of the
first 200 terms of the infinite series:
5 13 21 29
--- + ---- + ---- + ---- + . . .
5 15 25 35
Your output should be:
SUM =
160.726200
Problem#13
Given an
= 3an - 1 -
2an - 2 for n
³ 2 , a0 = 1 , a1 = 2 . Write a program to
find the value of a15.
Your output should be:
A15 = 32768
Problem#14
Write a program to process the
orders of breads from a bakery. The first data line for your program should
contain the number of breads initially available at the bakery. The second data
line contains the number of orders and each of the other data lines contains
the number of breads for a particular order. Your program must read the data
and print next to each order request either the message FILLED or NOT FILLED
according to whether the current number of breads in the bakery is sufficient
or is not sufficient for that
order. After all the orders have been processed, the program should print out
the final number of breads available, the number of breads sold, and the number
of additional breads, if any, which must be baked to fill all outstanding
orders (i.e. all orders which have the message: NOT FILLED).
Use the data:
1000
6
300
150
600
400
160
100
Your output should be:
INITIAL NUMBER OF BREADS =
1000
LIST OF ORDERS:
300 FILLED
150 FILLED
600 NOT FILLED
400 FILLED
160 NOT FILLED
100 FILLED
FINAL NUMBER OF BREADS =
50
950 BREADS SOLD
710 ADDITIONAL BREADS NEEDED
Problem#15
Write a program that reads grades
of students in a section and finds the highest grade. Read at the
beginning an integer N which represents
the number of students in the section.
Problem # 16
Write a program that reads grades
of students in a section and finds the average of the section. Read at the
beginning an integer N which represents the number of students in the section.
Problem#17
Write a program that prints a
table of temperature conversions
between Celsius and Fahrenheit. The program should prompt the user to enter the
initial and final temperatures. It must print an error message and terminate if
the initial temperature is greater than the final temperature. Use an increment
of 10.
Note: C o = ( 5.0 / 9.0 )
* ( F o - 32 ).
Test your program with the data:
-30.0 50.0
Your output should be:
CELSIUS FAHRENHEIT
-30.000000 -22.000000
-20.000000 -4.000000
-10.000000 14.000000
0.000000E+00 32.000000
10.000000 50.000000
20.000000 68.000000
30.000000 86.000000
40.000000 104.000000
50.000000 122.000000
Problem#18
Write a program that prints a
power table for values from 1 to 20 in steps of 1. The powers needed are
2,3,4,5.
Your output
should look like:
A POWER TABLE
N N**2 N**3
N**4
N**5
1
1 1
1
1
2
4
8
16
32
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
.
.
.
3200000
Problem#19
Write a program to tabulate the function:
y =
f(x) + g(x)
for x = 1, 2, 3, . . . , 10. Where:
f(x) =
x 2 - 16
and
? 1 if f(x) < 0
g(x) = ? x 2 +
16 if f(x) = 0
î
0 if f(x) > 0
Note: The
function y must be written as a function subprogram
Your output should be:
X
Y
1 -14
2 -11
3 -6
4
32
5 9
6
20
7
33
8
48
9
65
10
84
Problem#20
Write a program that prints a
table for the trigonometric functions sine and cosine for angles between 00
to 1200 in steps of 150.
Use p = 3.14159
Your output should be:
ANGLE SIN COS
0 0.000000E+00 1.000000
15 2.588189E-01 9.659259E-01
30 4.999996E-01 8.660256E-01
45 7.071064E-01 7.071072E-01
60 8.660250E-01 5.000007E-01
75 9.659255E-01 2.588201E-01
90 1.000000 1.267591E-06
105 9.659262E-01 -2.588176E-01
120 8.660262E-01
-4.999986E-01
Problem#21
Write a program to tabulate the
function:
f(x,y) =
(x2 + y2) / (2x + 1)
for x = 0, 1, 2, 3 and y = 3, 5,
7 for each value of x.
Note: The function f must be
defined as a statement function.
Your output should be:
X
Y
F(X,Y)
0.000000E+00 3.000000 9.000000
0.000000E+00 5.000000 25.000000
0.000000E+00 7.000000 49.000000
1.000000 3.000000 3.333333
1.000000 5.000000 8.666667
1.000000 7.000000 16.666670
2.000000 3.000000 2.600000
2.000000 5.000000 5.800000
2.000000 7.000000 10.600000
3.000000 3.000000 2.571429
3.000000 5.000000 4.857143
3.000000 7.000000 8.285714
Problem#22
The least squares method can be
used to find the equation of the straight line y = mx + b that best fits experimental points: (x1,
y1) , (x2, y2) , (x3, y3)
, . . . , (xn, yn). m and b are given by the following
formulas:
n
n n
n ? xiyi
- ( ? xi )( ? yi
)
i = 1
i = 1 i = 1
m = ¾¾¾¾¾¾¾¾¾¾¾
n n
n ? xi
2 - ( ? xi ) 2
i = 1
i = 1
n
n n n
( ? xi
2 )( ?
yi ) - ( ? xi )( ? xiyi
)
i = 1 i = 1 i = 1 i = 1
b = ¾¾¾¾¾¾¾¾¾¾¾¾¾
n
n
n ? xi
2 - ( ? xi ) 2
i = 1 i = 1
Write a program which will prompt
for and read the values for N and then the coordinates of N points. The program then computes m
and b for the points.
Use the following data:
6
5.0 6.883
29.7 -51.13
48.4 -94.02
73.0 -150.0
98.0 -208.6
8.2 0.03
The data represents the
experimental points:
|
x |
5.0 |
29.7 |
48.4 |
73.0 |
98.0 |
8.2 |
|
y |
6.883 |
-51.13 |
-94.02 |
-150.0 |
-208.6 |
0.03 |
Your output should be:
M = -2.306003
B = 17.312800
**Problem#23
The value of the integral:
b
ò
f(x) dx
a
can be approximated by the
summation:
(h / 3) * ( f(x0) + 4f(x1) + 2 f(x2)
+ 4 f(x3) + . . . + 2 f(xn - 2) + 4 f(xn - 1)
+ f(xn) )
where: x0 = a , x1 = a + h , x2 = a
+ 2h , . . . , xn - 1 = a
+ (n - 1)h , xn = b
and h = (b - a) / N , where N is a positive even integer.
Write a program which prompts for
and reads the values for a , b , and N it then approximates the integral:
b
ò
sin(x) cos2(x) dx
a
Use the following data: 0.0 1.0 10
Your output should be:
APPROXIMATE INTEGRAL IS 0.2807647
NOTE: Your program must print an
error message if the value for N is invalid or if a
³ b.
**Problem#24
The value of the integral:
b
ò
f(x) dx
a
can be approximated by the
summation:
(h / 2) * ( f(x0) + 2f(x1) + 2 f(x2)
+ 2 f(x3) + . . . + 2 f(xn - 2) + 2 f(xn - 1)
+ f(xn) )
where: x0 = a , x1 = a + h , x2 = a
+ 2h , . . . , xn - 1 = a
+ (n - 1)h , xn = b
and h = (b - a) / N , where N is a positive integer.
Write a program which prompts for
and reads the values for a , b , and N it then approximates the integral:
b
ò
sin(x) cos2(x) dx
a
Use the following data: 0.0 1.0 100
Your output should be:
APPROXIMATE INTEGRAL IS 0.2807571
NOTE: Your program must print an
error message if the value for N is invalid or if a ³ b.