Building a Balanced Binary Search Tree
Objectives of this lecture
q Lean how to construct a balanced binary search tree from an
ordered list of data items
The Problem
q Suppose that we have a list
of data items already sorted (say in a file or a linked list).
q If we wish to make a search
on this list of items (or other operations such as add, change, delete, etc. ),
then it would be better if we could form a binary search tree.
q However, if we do this using
the insert
function we saw earlier, then the resulting list will be a chain.
q Thus, we need another insert
function that will generate a BST that is as bushy as possible.
q For example, for ordered
list of 31 values, we wish to form the following complete tree.
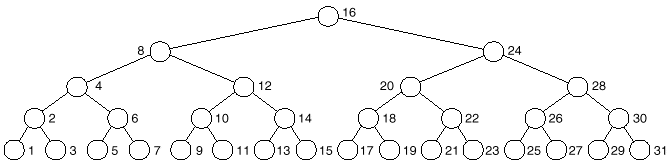
q Notice from the above figure
that:
Ø The labels of the leaves are all odd
Ø The labels of the nodes 1 label above the leaves is
divisible by 2 = 21
Ø The labels of the nodes 2 labels above the leaves is
divisible by 4 = 22
Ø The labels of the nodes 3 labels above the leaves is
divisible by 2 = 23
etc.
q Thus, generally, we have the
following:
q If a complete BST is labeled
inorder,
then each node is exactly n labels above the leaves, where n is the highest power of 2 divisible by the label.
Construction
q The following figure shows
how such a balanced BST may be constructed for a general case where the size of
the ordered list is not known.
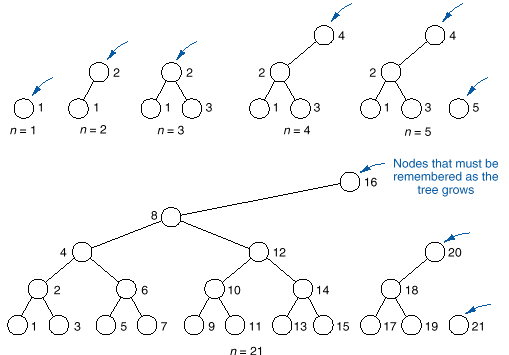
q Notice that to establish
future links, we need only remember pointers to one node on each label, the
last node processed on that level.
q We can achieve this
construction by using an array called lastnode to hold these pointers.
q As each new node arrives, it
is clearly the largest so far, so we could set its right pointer to NULL (at least
temporarily).
q Its left pointer is also NULL if it is a leaf node,
otherwise, it is the entry in the array lastnode which is one label lower
than the new node.
q We can treat the leaves in
the same way as other nodes if we place each pointer at level+1 in the lastnode where level is its actual level, so
that the leaves are on level 1 and we set lastnode[0] to be NULL.
q Also when a node arrives, it
may be the right child of some previous node or the left child of a node that
is yet to arrive. We can tell which
case occurs by checking the array lastnode.
q If the level of this new
node is denoted by level, then the level of its parents would be lavel+1. So we check the node at lastnode[level+1]. If its right link is still NULL, then its right child must
be the new node, if not, then its right child has already arrived and the new
node must be the left child of some future node.
q The following implement the
above ideas.
/*
Insert: insert newnode as the rightmost node of a partial tree.
Pre: newnode is a valid pointer of an entry to
be inserted into the
binary search tree.
Post:
newnode has been inserted as rightmost node of a partial binary
search tree.
Uses:
Power2.
*/
void
Insert(TreeNode *newnode, int count, TreeNode *lastnode[])
{
int level = Power2(count) + 1;
newnode->right = NULL;
newnode->left = lastnode[level-1];
lastnode[level] = newnode;
if (lastnode[level+1] &&
!lastnode[level+1]->right)
lastnode[level+1]->right = newnode;
}
q The following are the helper
functions used by Insert function above
#define ODD(x)
((x)/2*2 != (x))
/*
Power2: find the highest power of 2 that divides count.
Pre: x is a valid integer.
Post:
The function finds the highest power of 2 that divides x;
requires x != 0.
*/
int
Power2(int x)
{ int level;
for (level = 0; !ODD(x); level++)
x /= 2;
return level;
}
Connecting the branches
q We notice that if the number
of nodes is not a power of two minus 1 (2n-1) such as 31, by the end of the
insertion process, some branches would not be linked to the main tree.
q That is, we would have some
nodes whose right child is still NULL even though further nodes
that belongs to their right subtrees have arrived.
q The pointers of such nodes are
all in the array lastnode.
q To tie things up, the right
child of any node in lastnode that is currently NULL is set to the highest node
in lastnode
that is not already in its left subtree.
/*
ConnectSubtrees: connect free subtrees from lastnode[].
Pre: The nearly completed binary search tree has
been initialized. The
array last-node has been initialized
and contains the information
needed to complete the binary search
tree.
Post:
The binary search tree has been completed.
*/
void
ConnectSubtrees(TreeNode *lastnode[])
{ TreeNode
*p;
int
level, templevel;
for (level = MAXHEIGHT-1; level > 2
&& !lastnode[level]; level--)
; /* Find the highest node: root. */
while (level > 2) { /* Levels 1 and 2 are already
OK. */
if (lastnode[level]->right)
level--; /* Search for highest dangling node.*/
else { /* Right subtree is undefined. */
p = lastnode[level]->left;
templevel = level - 1;
do { /* Find highest entry not in left subtree. */
p = p->right;
} while (p && p ==
lastnode[--templevel]);
lastnode[level]->right = lastnode[templevel];
level = templevel;
}
}
}
Finding the root
q After connecting all the
branches, we can use the following function to find the root node.
/*
FindRoot: find root of tree (highest entry in lastnode).
Pre: The array lastnode contains pointers to the
occupied levels of
the binary search tree.
Post:
Return a pointer to the root of the newly created binary search
tree.
*/
TreeNode
*FindRoot(TreeNode *lastnode[])
{ int level;
for (level = MAXHEIGHT-1; level > 0
&& !lastnode[level]; level--)
;
if (level <= 0)
return NULL;
else
return lastnode[level];
}
Putting them all together
q The following function makes
use of the above functions to perform the building process.
/*
BuildTree: build nodes from GetNode into a binary tree.
Pre: The binary search tree pointed to by root
has been created.
Post:
The tree has been reorganized into a balanced tree.
Uses:
GetNode, Insert, ConnectSubtrees, FindRoot.
*/
TreeNode
*BuildTree(void)
{
TreeNode *newnode;
int count = 0; /* number of nodes so far */
int level; /* number of steps above leaves */
TreeNode *lastnode[MAXHEIGHT]; /* pointers to last node on each
level*/
for (level = 0; level < MAXHEIGHT;
level++)
lastnode[level] = NULL;
while ((newnode = GetNode()) != NULL)
Insert(newnode, ++count, lastnode);
newnode = FindRoot(lastnode);
ConnectSubtrees(lastnode);
return newnode; /* Return root of the tree. */
}
Analysis