Review of Searching Methods
Objectives
of this lecture
q Review two methods of
searching
q Introduce the concept of
Algorithm analysis
Introduction
q Information retrieval is one
of the most important applications of computers
q It usually involves giving a
piece of information called the key, and asked to find a record
that contains other associated information.
q This is achieved by first
going through the list to find if the given key exists or not, a process called searching.
q Searching ( and sorting) is
usually a time-consuming process, and is therefore a good candidate for
learning algorithm analysis.
q Searching can be external (if the data is contained
on a disk, tape, CD-ROM, etc) or internal (if the data is contained
in the memory). We shall restrict our
discussions to internal searching.
q We shall assume the
following declarations throughout this lecture.
#define MAXLIST ….
typedef …. KeyType;
typedef struct { .….
KeyType key;
…….
} ListEntry;
typedef struct {int count;
ListEntry entry[MAXLIST];
} List;
Note that KeyType could be of type int, float, or
string (char *).
q We shall adopt the
convention of returning the index (location) of the search key if it exists or –1 if it does not exists.
Macros:
q In searching, we often need
to compare between two keys to determine which comes fist. For numeric keys, we use the operators ‘<’ and ‘==’. However, for string keys, we must use the function strcmp().
q However, we would like to
code our algorithms such that they work in both cases.
q One method of achieving this
is to introduce functions such as:
Boolean EQ (KeyType key1, KeyType
key2);
Boolean LT (KeyType key1, KeyType
key2);
q However, this method is not
efficient since it involves a function call each time a pair of keys is
compared.
q Fortunately, C provides a
feature that allows us to code these functions without the need for functions
calls – macros.
q Macros are like functions –
they are called with actual parameters and they return some result.
q However, unlike functions,
they are not handled by the compiler, but by the C pre-processor.
E.g. The following macro
computes a square of a given argument:
#define
square(x) (x)*(x).
Notice that the parenthesis in (x)*(x) are necessary in case the
argument is an expression.
If the definition were: #define
square(x) x*x
the call square(a+b) would be evaluated as: a+b*a+b
q The macros we need for the
comparison of keys are:
For numeric keys
#define EQ(a,b) ((a) == (b))
#define
LT(a,b) ((a) < (b))
For string keys
#define EQ(a,b) (!strcmp((a),(b)))
#define LT(a,b) (strcmp((a),(b)) < 0)
Sequential
Search
q This is the simplest
searching method. It simply scans the
list from the beginning until the search key is found or the end of the list is
reached.
/* SequentialSearch: contiguous version.
Pre:
The contiguous list has been created.
Post: If target exists, the function
returns its location (success).
Otherwise the function returns -1 (failure).
*/
int SequentialSearch(List list,
KeyType target)
{
int location;
for (location = 0; location < list.count; location++)
if (EQ(list.entry[location].key, target))
return location;
return -1;
}
Informal Analysis of Sequential Search:
q The significant work for
this algorithm is done inside the loop.
For each pass through the loop, one key is compared with the target.
Other statements are also executed but they all depends on the key comparison. Thus, the amount of work done by the algorithm
depends on the number of key comparisons made.
q This number depends on if
and when the target is found as follows:
1.
Unsuccessful search: This requires n
comparisons
2.
Best case: search element at first
position; this requires only one comparison.
3.
Worst case: search element at last
position; this requires n comparisons.
4.
Average case: Assuming each element is as
likely as any other in the list, then the average number of comparisons
required for a successful search is: Sum up the number of comparisons required
for each element and then divide by n:
(1+2+3+...+n)/n = (½n(n+1))/n = ½(n+1)
Binary
Search
q For an ordered list, it is a
waste of time to look for an item using linear search (it would be like looking
for a word in a dictionary sequentially).
In this case we apply binary search – more efficient.
q Binary search works by
comparing the target with the item at the middle of the list.
This leads to one of three results:
Ø The middle item is the
target – we are done.
Ø The middle item is less than
target – we apply the algorithm to the upper half of the list.
Ø The middle item is bigger
than the target – we apply the algorithm to the lower half of the list.
q This process is repeated
until the item is found or the list is exhausted.
q The following functions implements
this approach:.
/* BinarySearch: a version of binary
search.
Pre: The contiguous list has been created.
Post: If target exists, the function
returns its location (success).
Otherwise the function returns -1 (failure).
*/
int BinarySearch(List list, KeyType
target)
{
int bottom, middle, top;
top = list.count - 1; //
Initialize bounds to cover entire list.
bottom = 0;
while (top >= bottom) { /*
Check terminating condition. */
middle = (top + bottom) / 2;
if (EQ(target, list.entry[middle].key))
return middle;
else if (LT(target, list.entry[middle].key))
top = middle - 1;
// Reduce to the bottom half of the list
else
bottom = middle + 1;
// Reduce to the top half of the list.
}
return -1;
}
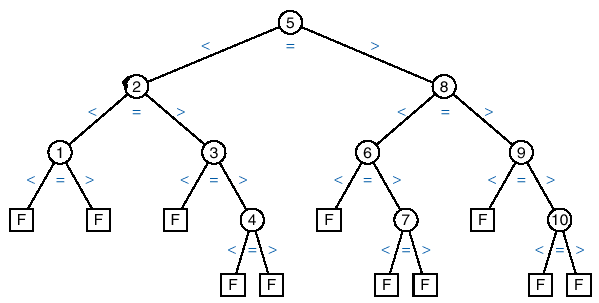
Informal Analysis of Binary Search:
q The easiest way to see how
binary search works is by drawing its comparison tree.
q This is done by tracing the
action of an algorithm, representing each comparison of keys by a vertex and
the possible outcome of the comparison are represented as branches.
q The following figure shows the comparison tree for binary search algorithm for a list of 10 elements: