INFORMATION
& COMPUTER SCIENCE DEPARTMENT, KFUPM
ICS
202: DATA STRUCTURES
LAB#12:
Implementation of Open Hashing
Methods
Objectives:
1. To put into practice the concepts learnt in the lectures on Hashing, including
a. Collision
b. Collision resolution schemes
2. To implement different collision resolution techniques under open addressing hashing:
a. Linear probing
b. Double hashing
c. Quadratic probing
- To experiment with the
insert(), find() and withdraw() operations in open hash
tables.
1. Downloadables:
Download lab12.zip and unzip it under the ics202
main folder.
After unzipping, the following files will be updated/added to the ics202 package:
AbstractHashTable.java
HashTable.java
OpenScatterTable.java
The following files will be placed in the ics202.lab12 sub-package:
OpenScatterTableTest.java
OpenScatterTable2.java
OpenScatterTable3.java
OpenScatterTable4.java
2. Task1
Study each of the files
AbstractHashTable.java, HashTable.java,
OpenScatterTable.java, and OpenScatterTableTest.java
carefully.
NOTE: Usually the objects inserted in a hash-table are Association objects. To simplify the lab tasks, we will use Integer objects.
3. Task2 (Linear probing)
Go through the file OpenScatterTableTest.java and complete the missing code as indicated by the comments in that file. Use a hash-table of size 13. After that, compile the file and run it. Choose option 4 to display the contents of the Hash table. You should get the following output:
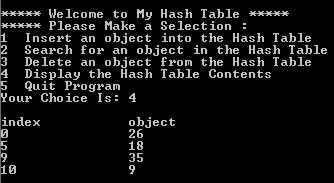
Note: The output agrees with the following computations:
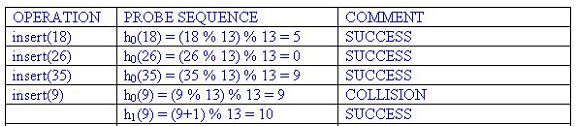
4.
Task3 (Linear probing)
Complete the class OpenScatterTable2 (in ics202.lab12 sub-package) that extends OpenScatterTable as indicated by the comments in that file. Your must also modify the OpenScatterTableTest.java program so that it calls an appropiate transactionReport method after each successful or unsuccessful operation. A sample session of the program is:
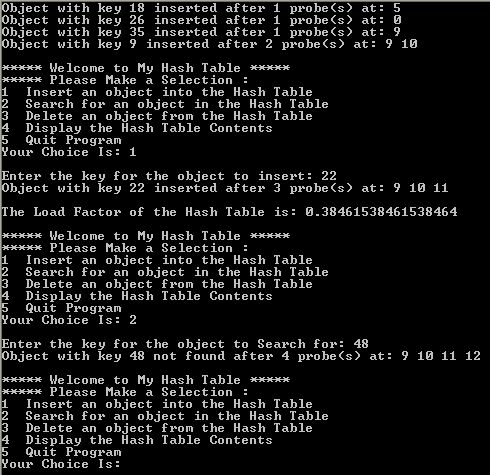
This indicates that the object 22 was inserted at location 11 of the Hash table after three probes at location 9, 10, and 11. It also indicates that the object 48 was not found in the Hash table after four probes at locations 9, 10, 11, and 12.
Note: You need to use try-catch blocks when calling the insert and withdraw methods.
withdraw(35), find(9), insert(64), insert(47), and find(35)
in this order. Your output must agree with the the following
computations:
5. Task
4 (Double hashing and Quadratic probing)
So far, we have been using linear probing technique for collision resolution. That is, we have used probing sequence:
hi(key) =
(h(key) + c(i)) % tableSize, where c(i) = i, for i = 0,1,2,…, tableSize-1.
and h(key) = key % tableSize
Now, you will implement and experiment with the other collision resolution schemes covered in the lectures.
a. Double hashing, with c(i) = i*hp(key), where:
h(key) = key % tableSize
hp(key) = 1 + (key % (tableSize - 1))
by completing the class OpenScatterTable3 that extends OpenScatterTable2 as indicated in the comments in that file.
Use the following problem to test your program: Insert the keys in the array {18, 26, 35, 9, 64} followed by the keys 47, 96, 36, and 70 in this order, in an empty hash table of size 13.
Your output must agree with the following computations:
b. Quadratic probing, with :
c(i) = ±i2 for i = 0,1, 2,…,(tableSize - 1)/2
by completing the class OpenScatterTable4 that extends OpenScatterTable2 as indicated in the comments in that file. Use the
following problem to test your program:
order, in a hash table of size 7 using quadratic probing with the hash function: h(key) = key % 7
Your output must agree with the following computations:
h1(7) = (0 + 12) % 7 = 1 collision