Copyright © 2005 Elsevier B.V. All rights reserved.
Crack propagation trajectories for rocks under mixed mode I–II fracture
King Fahd University of Petroleum and Minerals, Civil Engineering Department, Box 368, Dhahran 31261, Saudi Arabia
Received 2 April 2005;
Abstract
Propagation of a crack in engineering materials including rocks can cause failure. Knowledge of the stress state under which a crack can propagate, and the trajectory it may follow during its growth are thus very important for the stability of rock masses/materials and for the safe design of structures in/on rocks. In this paper, the crack initiation angle and subsequent crack propagation path are experimentally investigated for limestone rock specimens. This investigation was conducted under various mixed mode I–II loading conditions, including pure mode-I and pure mode-II.
This study includes conducting diametrical compression tests on notched Brazilian disk specimens. Moreover, the effect of confining pressure and temperature on crack initiation and propagation were also studied. The experimental results were compared with theoretical predictions of crack initiation angle. The results showed that limestone behaves in brittle fashion, and the effects of confining pressure and temperature on failure trajectories were not significant. Generally, the crack initiation angle can be predicted by the maximum tangential stress criterion. However, for notched Brazilian disk with high value of crack orientation with respect to loading direction, crack does not propagate from the tip of the crack. This important observation indicated that the tensile-strength failure can become more critical than the fracture-toughness failure.
Keywords: Limestone; Fracture toughness; Mixed-mode I–II; Crack initiation; Crack trajectories
Article Outline
- 1. Introduction
- 2. Background
- 3. Geology and rock description
- 2. Background
- 3.1. Geology
of the area
- 3.2. Rock properties
- 4. Experimental investigation
- 4.1. Sample
preparation
- 4.2. Testing
- 5. Results and discussions
- 5.1. Crack
deformation
- 5.2. Crack initiation
- 5.3. Crack propagation path
- 5.2. Crack initiation
- 6. Conclusions
- Acknowledgements
- References
- Acknowledgements
1. Introduction
When a solid body with a pre-existing crack is subjected to externally applied forces, stresses concentrate at the vicinity of the crack tip. If the stress exceeds a certain critical value, the crack starts propagating outward resulting in the failure of the body. Based on the loading type, there are three basic crack propagation modes in a fracture process, namely: Mode I (tension, opening), Mode II (shear, sliding), and Mode III (shear, tearing). Accordingly, a crack can propagate according to any of these modes or a combination of them. In fact the combination of mode-I and mode-II (i.e. mixed mode I–II) is more common in rocks (Whittaker et al., 1992).
Experimental work has been conducted to predict the initial crack growth angle and the crack propagation path in various materials (Erdogan and Sih, 1963, Vallejo, 1987, Ingraffea, 1977 and Pustejovsky, 1979). Nevertheless, data for rocks is very limited. Xediakis et al. (1997) used simply supported beams for the study of mixed mode crack propagation in marble. Such specimens require extensive machining for sample preparation. To overcome such difficulties, a centrally notched disk type specimen under diametrical compression has been proposed and extensively used in the past for fracture toughness study of brittle materials including rocks (Awaji and Sato, 1978, Atkinson et al., 1982, Sanchez, 1979, Shetty et al., 1986, Fowell and Xu, 1994 and Krishnan et al., 1998). This specimen geometry is very convenient for mixed mode I–II. Chen et al. (1998) have numerically studied the mixed mode failure trajectories for rock using boundary element method. But his study is limited to only pure mode-I and pure mode-II failure, and does not cover the whole spectrum of the mixed mode I–II failure. Therefore, crack propagation for mixed mode failure in diametrically compressed disk requires further investigation.
The above studies however do not consider more than one crack, and consequently, crack interaction is not covered when more than one crack is present in the loaded rock specimen. These topics are beyond the scope of this present study. Vallejo (1987) investigated the influence of fissures on the failure of stiff clays under shear; and Vallejo (1989) studied the effect of fissure parameters on the compressive strength of stiff clays.
In this work, centrally straight-notched Brazilian disk (CSNBD) specimens, with various crack inclinations, were used to study the crack propagation behavior under mixed mode I–II loading. These specimens have a central notch and were loaded with diametrical compression (Fig. 1). The fracture toughness for such specimens was reported by Khan and Al-Shayea (2000) and Al-Shayea et al. (2000), and the fracture toughness envelope was reported by Al-Shayea and Khan (2001). In this paper, the failure path in such specimens were traced and compared with the theoretical predictions.
2. Background
There are numerous failure criteria for crack initiation and propagation under mixed mode I–II loading condition. The most popular ones are: (1) the maximum tangential stress (σ) criterion, (2) the maximum energy release rate (G) criterion, and (3) the minimum strain energy density (S) criterion. The available experimental data shows that no distinct theoretical failure criterion is applicable to all cases. Also, these criteria imply that mode-I fracture toughness (KIC) is larger than mode-II fracture toughness (KIIC), while experimental data show the opposite. Moreover, due to the fact that the existing failure criteria were developed based on the tensile loading rather than the compressive, they hold good only in the positive region (crack opening) and cannot predict the fracture behavior in the negative zone (crack closure).
Many researchers have recommended using empirical relations for practical applications. Huang and Wang (1985) and Sun (1990) have used one of three empirical equations of straight line, ellipse, and homogenous quadratic to fit the experimental fracture toughness data in the (KI / KIC)–(KII / KIIC) plane. Also, an exponential relationship was used by Awaji and Sato (1978), and a polynomial fitting were reported by Al-Shayea and Khan (2001).
The theory of maximum tangential stress (σ) assumes that crack propagates along a path normal to the direction of maximum tangential stress. Apart from the nature of the stresses at the crack tip, the crack propagation also depends upon the degree of the sharpness of the crack tip. Tirosh and Catz (1981) analyzed the problem of crack propagation in a body with a preexisting crack and subjected to compressive forces taking into consideration the effect of the crack tip radius. However, the application of linear elastic fracture mechanics (LEFM) to brittle materials, like rocks, is still not fully compatible, and this area needs further study (Degiorgi et al., 1995).
Since the failure load and the failure path in the mixed mode loading
condition depend on the nature of stresses acting at the crack tip,
determination of stress field in a specimen subjected to externally applied
forces is the first point in tracing the crack propagation path. Assuming a
homogeneous, isotropic, and linearly elastic material, stress state for an
uncracked disk under diametrical compression was formulated by Atkinson
et al. (1982). The stress components in polar coordinates are the radial
stress (σr), the tangential stress
(σβ), and the shear stress
(σrβ) (Fig.
2); and they are given in the following forms:
where,
When a CSNBD specimen is loaded diametrically (Fig. 1) with the crack inclined at an angle β with respect to the loading direction, the state of stresses will be altered by the presence of the crack. However, the above stresses (Eqs. Figs. (1), (2) and (3)) for uncracked disk can be helpful in predicting the direction of crack propagation in a cracked disk under mixed mode I–II loading.
Failure could be along the grains, along the cementation between the grains, or splitting the grains from the cementing material. When CSNBD specimens are subjected to diametral compression, tangential stresses at the crack tip may be tensile or compressive depending upon the crack inclination angle. This tangential stress, in combination with varying shear stresses at the crack tip, will cause the crack to propagate along a certain trajectory that results in an abrasive action along the failure surface. This abrasion could cause damage or crush the grains along the failure path depending upon the relative amount of each of these two stresses, in addition to the radial stress.
3. Geology and rock description
3.1. Geology of the area
Rock samples used in this investigation were obtained from a limestone rock formation outcropping in the Central Province of Saudi Arabia. The investigated limestone rock belongs to “Khuff” formation, which relates to age of early Triassic to late Permian age (215 to 270 M.Y.B.P.). A general trend of the sedimentary rock formations in the region is shown in Fig. 3. These formations dip gently and uniformly northeast, east and southeast, with value of about 1° (Powers et al., 1963). These form the Arabian shelf, which occupies central and eastern parts of the Saudi Arabia. The western part houses the Arabian shield. Tectonically, Saudi Arabia falls within the stable region; between the great rift–fault system of the Red Sea and the Taurus–Zagros–Oman chain of mountains.
The structural geology for Khuff formation indicates that it outcrops at various places in the Central Province of Saudi Arabia, with an altitude reaching hundreds of meters above the sea level, and it dips toward the east to a depth of about two to four thousand meters below sea level in the Eastern Province. At that depth, it houses the Ghwar field, the world largest petroleum reservoir producing oil and gas from multi-reservoir zones in the Khuff formation.
The generalized lithology of the Khuff formation consists of layers of limestone, claystone, dolomite, anhydrite, and sandstone. Previously, it was reported that Khuff formation consists of few members making a total thickness of about 171 m (Powers et al., 1963). More recently, Al-Jalal (1994) reported that the thickness of the Khuff formation increases basinward (from southwest to northeast) from 450 to 975 m, with a thickness of about 500 m in the Ghawar field. The carbonate and anhydrite sequence upward is subdivided into four units of alternating anhydrite and carbonate pairs (Powers et al., 1963). These units represent the four major tidal cycles (Al-Jalal, 1994).
3.2. Rock properties
Blocks of limestone rock were obtained from a highway side cutting the outcrop of Kuff formation in Gassim area, Saudi Arabia (Fig. 4). The mineralogical composition of this rock was determined by X-ray diffraction (XRD) analysis (Fig. 5). Results indicated that this rock is very pure limestone (99% CaCO3). Visual inspections indicated that the investigated limestone rock is a very homogenous, isotropic, beige (tan) in color, muddy limestone. It is very tight and lacks any pores or microcracks visible under a polarizing microscope, and therefore it has a negligible porosity. This limestone is microcrystalline, fine-grained, with crystalline texture. It is free from bedding planes, fossils, and minor constituents. It is dry, with no moisture content. The tested specimens were taken from the middle of the blocks to avoid any possible boundary effects.
.gif)
| Full-size image (87K) |
Fig. 4. Khuff formation outcropping in Gassim area, sample collection location.
Its physical properties included a dry density of 2.586 gm/cm3, a specific gravity of 2.737, a void ratio of 0.055, and porosity of 5.4%. The mechanical characteristics of this limestone rock included a uniaxial unconfined compressive strength of 105 MPa, a tensile strength of 2.31 MPa, a modulus of elasticity of 54 GPa, and a Poisson's ratio of 0.276, Khan and Al-Shayea (2000). The values of stress intensity factors for modes I and II (KIC and KIIC) are 0.42 and 0.92 MPa m1/2 for ambient condition; 1.57 and 2.18 MPa m1/2 under confining pressure (σc) = 28 MPa at ambient temperature; 0.52 and 1.00 MPa m1/2 at a temperature (T) = 116 °C, Al-Shayea et al. (2001).
4. Experimental investigation
4.1. Sample preparation
Coring was made through the rock blocks to obtain samples. The cores were then sliced into smaller disks using a high-speed circular saw. The disks were 98 and 84 mm in diameter, and 22 mm in thickness. A straight notch was made at the center of each disk using a 0.25 mm thick diamond impregnated wire saw for a notch length of 30 mm (i.e., a / R = 0.3), Khan and Al-Shayea (2000) This made the crack tip to be a semicircular with a radius (ρ) equal to 0.125 mm. A crack extensometer, capable of measuring crack extension down to 2040 divisions of 1 mm, was glued to the specimen surface at the crack mouth (Fig. 6).
4.2. Testing
A strain-controlled loading frame having a capacity of 100 KN was used for the load application with a strain rate of 0.08 mm/min. Disk specimens were diametrically loaded with different values of the crack inclination angle (β) ranging from 0° to 75° with a 15° increment. Loading was continued till failure. Tests were made at ambient conditions, at high confining pressure (σc) of 28 MPa, and at high temperature of 116 °C. Other details of the experimental setup were reported Al-Shayea et al. (2000). Among others, the vertical load and the crack deformation were continuously recorded during the test using a computerized data logger. Crack deformation was monitored only at ambient conditions.
The effect of mixed mode I–II loading condition on the nature of the broken surface was investigated using Scanning Electron Microscope (SEM) analysis. SEM was utilized to investigate the nature of the cracked surface. The fractured surface of the specimens for different crack orientations could reveal some information about the failure type and the influence of the crack orientation on the grain crushing along the failure surface. For this purpose, the specimens tested at a crack inclination of 0°, 15°, 30°, 45°, and 75° were studied for qualitative assessments.
5. Results and discussions
5.1. Crack deformation
Crack deformation was monitored during testing the CSNBD specimens under ambient conditions. Fig. 7 shows typical crack deformation responses at the center of the disk, for various crack inclination angles. It can be seen that the crack opened for crack inclination (β) of up to 30°. This is because at low value of β, mode-I crack tip stress is tensile in nature, which causes the crack to open. For higher values of β (> 30°), mode-I stress becomes compressive, thereby causing the crack to close. Samples tested at a crack inclination of more than 30° experienced a compressive tangential stress at the crack tip, which increases with increasing β, and the mode-I component becomes negative (i.e., crack closing or compression). The crack closure becomes more pronounced at higher crack inclination of 60° and 75°.
The maximum crack deformation is plotted against the crack inclinations, β, in Fig. 8. The maximum crack closure was observed at a crack inclination of 75°. The amount of this closure is around 0.113 mm, which is much less than width of the notch (0.25 mm). This means that the two sides of the notch did not come in contact with each other before failure.
5.2. Crack initiation
Crack initiation includes two components: crack initiation point (location)
and crack initiation angle (direction). The crack initiation point is usually
expected to be the tip of the pre-existing notches in the CSNBD specimens. The
notch remained open during the diametrical compression loading, until the load
increases beyond a certain value, at which the cracks initiated at the tip of
the notch and propagated very rapidly along a curvilinear path towards the
points on the boundary of the disk where the compression load was applied. When
the propagating crack reached the upper and lower boundaries of a sample, the
sample failed and broke into two pieces, as shown in Fig.
9. The crack initiated at the tip of the notch for specimens with values of
β up to 60° only. However, for specimen with β = 75°,
the crack did not initiate from the notch tip. This phenomenon was common for
all sizes of specimens tested at ambient and at different conditions of
temperature and confining pressure. Therefore, for high values of β
(higher than 60° to 75°), the specimen failed in a tensile splitting mode rather
than in a fracture toughness mode. Note that the tensile strength
(σt) for uncracked disks is:
Fig. 10 shows a plot of the normalizing stress (σo = P / πRB) at failure for various values of β. For low values of β (less than 30°), the values of the normalizing stress (σo) are less than the tensile strength (σt = 2.31 MPa). This is because mode-I is positive (opening, tensile) for this range of β. Notice that mode-I switches from positive (opening, tensile) to negative (closing, compression) at a value of β equals to 29°, Al-Shayea et al. (2000). On the other hand, for 30° < β < 60°, the values of σo is greater than σt. This can be attributed partially to the fact that mode-I is negative (closing, compressive). Additionally, the existence of the notch with such inclination might have prevented the development of tensile splitting mode of failure, leading to such high values of σo. For β = 75°, the value of σo is equal to σt, which is due to the fact that the specimens fail in a tensile splitting mode. At such orientation, the specimens behave in a way disregarding the existence of the notch. A correlation between fracture toughness and tensile strength of this type of rocks was presented by Al-Shayea et al. (2001).
.gif)
| Full-size image (15K) |
Fig. 10. Normalizing stress (σo) at failure for CSNBD specimens under mixed mode I–II loading.
The crack initiation angle (θ) is the angle by which the crack extension deviates from the direction of the original notch (Fig. 11). The crack extension angle (θ) has been manually measured from the broken specimens. Data were plotted in Fig. 12 versus the crack orientation angle (β). Results are compared with the theoretical analysis of crack propagation under mixed mode I–II loading condition based on the maximum tangential stress (σ-criterion). The crack initiation angle for different specimen size (i.e. 98 and 84 mm diameter) tested at confined conditions was observed to be in the same range as of those tested at ambient conditions. The crack propagation seems to be independent on the specimen size and testing conditions of temperature and confining pressure. The experimental results fall close to the theoretical line of the maximum tangential stress criterion for which ρ / a = 0.1, where ρ / a is a measure of the degree of crack tip sharpness and is the ratio of the radius of curvature at the crack tip (ρ) to half of the crack length (a). For an ideally sharp crack tip, ρ / a = 0. For the tested specimens, ρ / a = 0.125 / 15 ≈ 0.008. The crack initiation is more sensitive to the degree of crack sharpness at small crack orientations with respect to the loading plane. At higher crack orientations (β > 30°), the degree of crack sharpness has no significant effect on the crack initiation angle.
For comparison purposes, the values of θ for uncracked disk are also plotted in Fig. 12 versus the orientation angle (β). These were obtained from the normalized stresses (σr / σo), (σβ / σo), and (σrβ / σo), at a location corresponding to that of the crack tip for (a / R) = 0.3, which are calculated using Eqs. Figs. (1), (2) and (3) and shown in Table 1, for selected values of β ranging from 0° to 90°. Using these normalized stresses for each value of β, Mohr–Coulomb failure criterion was used to obtain the direction of the minimum principal stress with respect to the direction of the crack (θ) as given Table 1, which is measured from the plane on which tangential stress acts. This can be correlated with the direction of the crack propagation for cracked specimens.
5.3. Crack propagation path
The patterns of the failure path under the mixed mode I–II condition were traced and plotted in Fig. 13. The crack propagation trajectory is dictated by the stress state at any point. The distribution of stresses in an uncracked disk under diametrical compression are obtained from Eqs. Figs. (1), (2) and (3), and presented in terms of the stress contours in Fig. 14 for the normalized stresses (σβ / σo), (σr / σo), and (σrβ / σo), respectively.
.gif)
| Full-size image (11K) |
Fig. 13. Failure trajectories for the CSNBD specimens under mixed mode I–II loading.
.gif)
| Full-size image (154K) |
Fig. 14. Contours of the normalized stresses for uncracked Brazilian disk under diametrical compression, (a) tangential stresses, (b) radial stresses, (c) shear stresses.
When there is a crack in the center of the disk, stresses will concentrate at the crack tip. If these concentrated stresses reach a critical value, failure occurs due to propagation of the preexisting crack initiating from the tip and extending towards the loading points. It can be anticipated from Fig. 14 that the stress distribution at the crack tip is expected to be a function of the crack length as well as its orientation with respect to the loading direction. By varying the crack orientation for a particular crack length, a variety of stress states and mixed mode failure patterns can be obtained.
The normalized stresses (σβ / σo), (σr / σo), and (σrβ / σo) for uncracked disk along a circumferential of r / R = 0.3 are plotted in Fig. 15. The distribution of tangential stress (Fig. 15-a) is symmetrical about both horizontal and vertical axes. In the first quadrant of the disk, the tangential stress is tensile for values of β ranging from 0° to 24.5°, with a maximum tensile value of β = 0°. Then it becomes compressive for values of β ranging from 24.5° to 90°, with maximum compression value of β = 90°. Notice that mode-I fracture toughness switches from tensile to compression at β ≈ 29°, Al-Shayea et al. (2000). Also, the distribution of radial stress (Fig. 15-b) is symmetrical about both horizontal and vertical axes. In the first quadrant of the disk, the radial stress is compression for values of β ranging from 0° to 57.4°, with maximum compression value of β = 0°. Then it becomes tensile for values of β ranging from 57.4° to 90°, with a maximum tensile value of β = 90°. On the other hand, the distribution of shear stress (Fig. 15-c) is positive in the first and third quadrants of the disk, and negative in the second and third quadrants, as per the sign convention given in Fig. 2. In the first quadrant, the shear is zero at both β = 0° and 90°, and it has a maximum value at β = 35.2°. For comparative purposes, Fig. 15-d shows the variation of all stress (tangential, radial, and shear), along r / R = 0.3 in the first quadrant of the disk.
Crack propagation path can be investigated by superimposing the experimental failure trajectories (Fig. 13) over the contours of the theoretical tangential, radial, and shear stresses for uncracked disk (Fig. 14). For pure mode-I (β = 0°), the crack propagated under the influence of the tangential stress (tension). Mixed mode I–II can be divided into three ranges. For 0° < β < 30°, the tangential stress is tensile at the crack tip, and the shear stress causes a sliding action along the plane of the notch. For 30° < β < 60°, although the tangential stress at the notch tip is compressive, but the radial stress is also compressive, and the shear stress causes a sliding action along the plan of the notch. For both above ranges, the crack starts from the tip of the notch, then it deviates under the action of the stress state towards the zone where the tangential stress is tensile (positive). The crack follows a curvilinear path, which is nearly perpendicular to the contours of the radial stresses. For β = 75°, the tangential stress at the crack tip are excessively compressive (crack closing), the radial stress is tensile, and the shear stress is low. The crack could not start from the tip, but it started where the tangential stress is tensile (at the center of the specimen) and it propagates along the loading direction. For 75° < β < 90°, the same behavior is expected, i.e. the tensile splitting mode with crack propagates not from the tip of the notch.
Fig. 16 shows the SEM micrograph for the crack orientation of 0°, 15°, 30°, 45°, 60°, and 75°, with 1000× magnifications. Micrograph for β = 0° shows the coarse nature of the cracked surface with sharp boundaries between grains, representing failure by splitting (pure opening mode). Micrograph for β = 15° shows the cracked surface produced by the combination of splitting (opening) and shear modes, which consists of coarse splitted grains, with some crushing at the grain boundaries. Micrograph for β = 30° shows some crushing of boundaries between grains, because failure is due to pure sliding shear. The nature of cracked surface for the sample tested at β = 45° and 60° shows smaller granular appearance representing higher degree of abrasion and grain crushing due to combinations of sliding and compression, with the degree of crushing and abrasion is more for the that at β = 60°. The sample tested at 75° failed along the diametrical line coinciding with the loading direction (i.e. failure did not initiate from the crack tip). Its micrograph appears to be the same as that tested at β = 0° revealing that the failure surface was created under the influence of pure tensile stresses.
.gif)
| Full-size image (210K) |
Fig. 16. Scanning Electron Microscopic (SEM) images of the fractured surface of CSNBD specimens with 1000× magnifications.
Fig. 16-a and f indicate that the grains are fine, with an average size of about 20 ìm, and they are very tight with very few pores. It also shows the crystalline texture.
6. Conclusions
For CSNBD specimens under diametrical compression, tangential stresses at the crack tip may be tensile or compressive depending upon the crack inclination angle. This tangential stress in combination with varying shear stresses at the crack tip will cause a crack to propagate in a variety of mixed mode I–II failures trajectories.
Generally, the crack propagation in mixed mode I–II can be predicted by the theory of maximum tangential stress, in the range of crack inclinations at which the crack closure is not considerable. However, at larger crack inclinations, the maximum tangential stress criterion fails to predict the direction of crack propagation, due to crack closure under compressive tangential stresses.
The results showed that limestone behaves in brittle fashion, and the effects of confining pressure and temperature on failure trajectories were not significant. However, for high values of crack orientation with respect to loading direction, crack does not propagate from the tip of the notch, but from the center of the specimen, similar to the case of tensile splitting for uncracked specimen. This important observation indicated that the tensile failure can become more critical than the fracture failure. Therefore, CSNBD specimen is not a good configuration for determining fracture toughness at large values of crack initiation angle.
-
- Notations
θ
- Notations
-
Crack initiation angle (degrees) with respect to crack original plane
-
σβ
-
Tangential stress at the crack tip at an angle β from loading direction
-
σc
-
Confining pressure
-
σr
-
Radial stress at an angle θ from the crack tip
-
σo
-
Normalizing pressure = P / πRB
-
σrβ
-
Radial shear stress at the crack tip at an angle β from loading direction
-
σt
-
Tensile strength
-
a
-
Half of the notch length
-
B
-
Thickness of the disk specimen
-
CSNBD
-
Central Straight Notch Brazilian Disk
-
D
-
Diameter of the disk specimen
-
KI
-
Mode-I stress intensity factor
-
KIC
-
Pure mode-I stress intensity factor
-
KII
-
Mode-II stress intensity factor
-
KIIC
-
Pure mode-II stress intensity factor
-
LEFM
-
Linear Elastic Fracture Mechanics
-
P
-
Load at failure
-
R
-
Radius of the disk specimen
-
T
-
Temperature
-
β
-
Crack inclination angle (degrees) with respect to the loading direction
-
ρ
-
Radius of curvature of the crack tip.
Acknowledgement
The author acknowledges the support of King Fahd University of Petroleum and Minerals for providing computing, laboratory, and editing facilities. He is also grateful to Mr. Khaqan Khan and Mr. Hasan Zakaria for their help in conducting the tests.

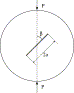
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)