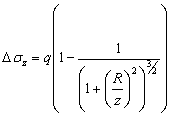HOMEWORK SOLUTION

 

HW #7

 

GEOTECHNICAL ENGINEERING I

 

(Question no. 6.25, 6.27, 6.28A, 6.33c..Al-Khafaji textbook)

 

 


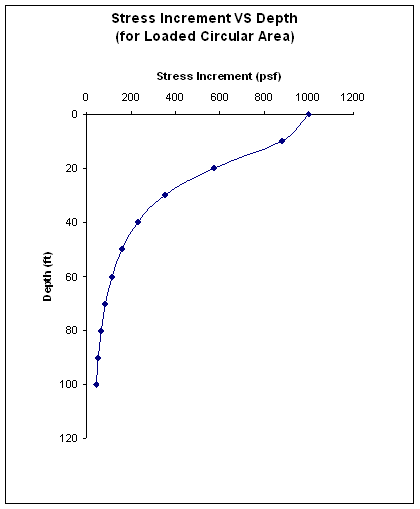
6.25 Calculate & plot vertical stress increment under the center of storage tank f =35 ft increment 10 ft up to 100 ft deep.

 

        Solution:

 

 

z

R/z

Dsz

0

~

1000

10

1.75

877.8735

20

0.875

573.7619

30

0.583333

355.5225

40

0.4375

231.0286

50

0.35

159.1462

60

0.291667

35 ft
 
115.264

70

0.25

86.92471

80

0.21875

100 ft
 
67.71145

90

0.194444

54.14606

100

0.175

44.23969

 

 

 

 

 

 

 

 

 

 

 

 

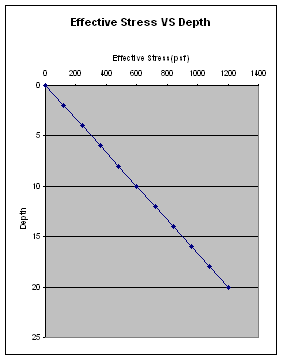
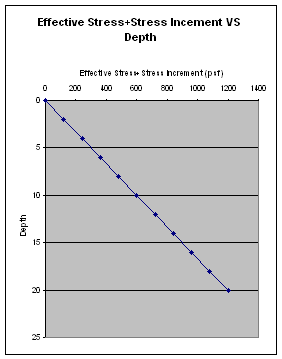
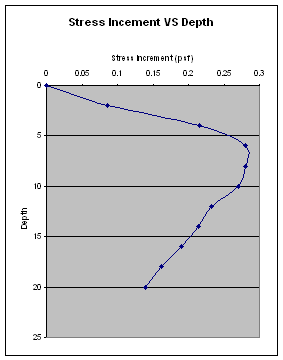
6.27 Calculate & plot vertical stress increment under point x. Plot effective overburdaned and effective overburdened + vertical stress increment!

 

Solution:

 

See the following calculation (tabled) and graphs:

           

q = 2 psf
 
    x

 

 

 



z (ft)

m(A1+A2)

n(A1+A2)

I(A1+A2)

Dsz(A1+A2)

m(A2)

n(A2)

I(A2)

Dsz(A2)

Dszx (psf)

Dseffective (psf)

Dseffective+Dsz (psf)

 

 

 

 

 

 

 

 

 

 

 

 

0

~

~

0.25

0.5

~

~

0.25

0.5

0

0

0

2

6

5

0.248

0.496

1

5

0.205

0.41

0.086

120

120.086

4

3

2.5

0.244

0.488

0.5

2.5

0.136

0.272

0.216

240

240.216

6

2

1.666667

0.228

0.456

0.333333

1.666667

0.088

0.176

0.28

360

360.28

8

1.5

1.25

0.21

0.42

0.25

1.25

0.07

0.14

0.28

480

480.28

10

1.2

1

0.19

0.38

0.2

1

0.055

0.11

0.27

600

600.27

12

1

0.833333

0.162

0.324

0.166667

0.833333

0.046

0.092

0.232

720

720.232

14

0.857143

0.714286

0.142

0.284

0.142857

0.714286

0.035

0.07

0.214

840

840.214

16

0.75

0.625

0.125

0.25

0.125

0.625

0.03

0.06

0.19

960

960.19

18

0.666667

0.555556

0.105

0.21

0.111111

0.555556

0.024

0.048

0.162

1080

1080.162

20

0.6

0.5

0.09

0.18

0.1

0.5

0.02

0.04

0.14

1200

1200.14

Note:

z                       = depth (2’ increment)

m,n                   = length,width of rect./square

I                       = Influence factor (figure 6.21 textbook)

Dsz(A1+A2)       = q (IA1+A2)

Dsz(A2)             = q (IA2)

Dszx                 = Dsz(A1+A2) - Dsz(A2) …stress increment at x

Dseffective         = z (gsat-gw)

 
 



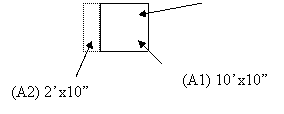
6.28a  Assumed depth increment 0,5,10,15,20,30 ft. Determine stress increment  versus depth for the footings.

 

            Solution:

           

z (ft)

m

n

I

Dszrect.(ksf)

z/r

x/r

I

Dszcirc.(ksf)

DszTotal.(ksf)

0

~

~

0.25

0.125

0

1.414

0.001

0.002

0.127

5

7

4

0.247

0.1235

0.5

1.414

0.06

0.12

0.2435

10

3.5

2

0.24

0.12

1

1.414

0.12

0.24

0.36

15

2.333333

1.333333

0.22

0.11

1.5

1.414

0.15

0.3

0.41

20

1.75

1

0.2

0.1

2

1.414

0.13

0.26

0.36

30

1.166667

0.666667

0.158

0.079

3

1.414

0.09

0.18

0.259

 

 

 

 

 

 

 

 

 

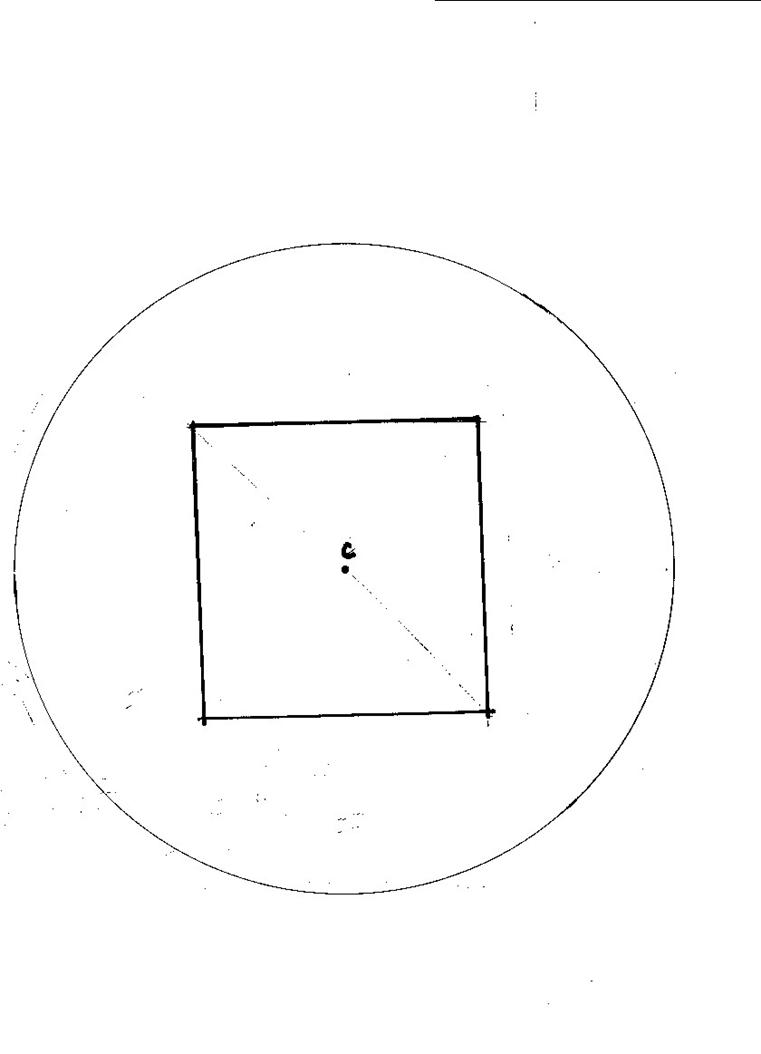
6.33c Using Newmark chart In=0.005 and scale z=5 cm

 

 

 

(a)    Depth increment 0 ft

Dsz = 200 x 0.005 x q = 1 x 128/(8x8) = 2 ksf

 

(b)   Depth increment 5 ft

Scale    5 ft = 5 cm   so that 1 ft = 1 cm

See graph 1.

            Nn = 116 (number of element using Newmark chart)

Dsz = In x Nn  x q = 0.005 x 116 x 2 ksf = 1.16 ksf

 

(c)    Depth increment 10 ft

Scale    10 ft = 5 cm   so that 1 ft = 0.5 cm

See graph 2.

            Nn = 54 (number of element using Newmark chart)

Dsz = In x Nn  x q = 0.005 x 54 x 2 ksf = 0.54 ksf

 

(d)   Depth increment 15 ft

Scale    15 ft = 5 cm   so that 1 ft = 0.33 cm

See graph 3.

            Nn = 38 (number of element using Newmark chart)

Dsz = In x Nn  x q = 0.005 x 38 x 2 ksf = 0.38 ksf

 

(e)    Depth increment 20 ft

Scale    20 ft = 5 cm   so that 1 ft = 0.25 cm

See graph 4.

            Nn = 33 (number of element using Newmark chart)

Dsz = In x Nn  x q = 0.005 x 33 x 2 ksf = 0.33 ksf

 

(f)     Depth increment 30 ft

Scale    30 ft = 5 cm   so that 1 ft = 0.167 cm

See graph 5.

            Nn = 24 (number of element using Newmark chart)

Dsz = In x Nn  x q = 0.005 x 24 x 2 ksf = 0.24 ksf

 

 

 

 

 

 

 

 

 

 

Graph 1.

 

Scale    5 ft = 5 cm   so that 1 ft = 1 cm

Nn = 116 (number of element using Newmark chart)
 

 

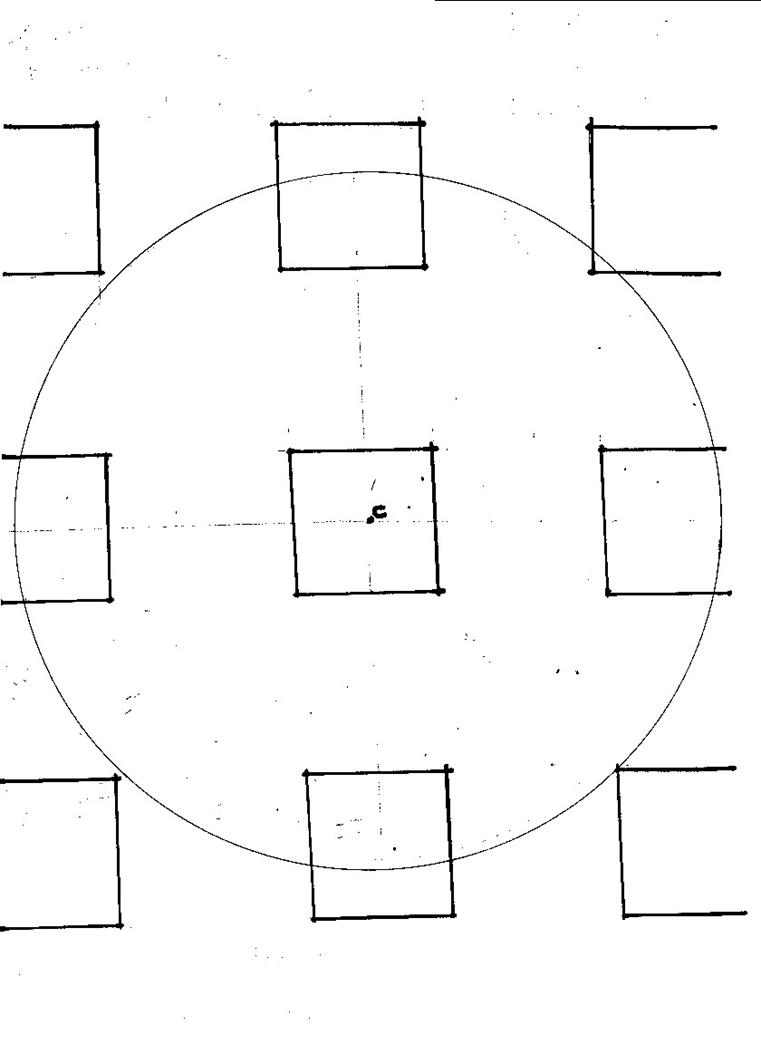
Graph 2.

 

Scale    10 ft = 5 cm   so that 1 ft = 0.5 cm

Nn = 54 (number of element using Newmark chart)
 

 

 

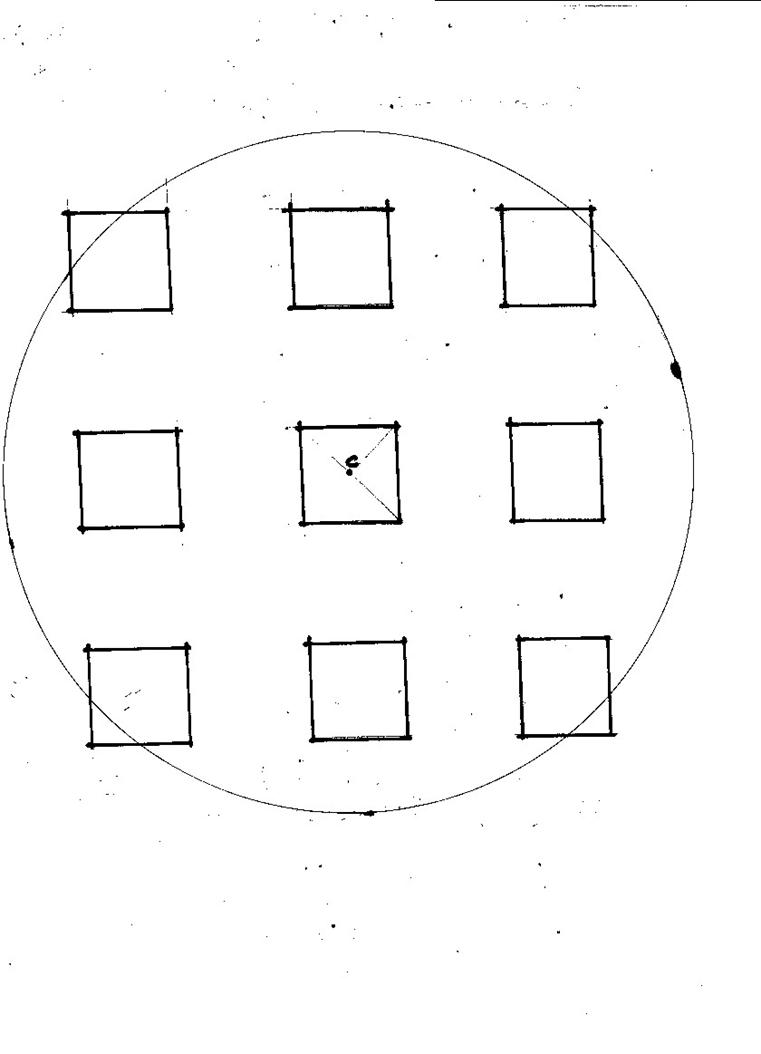
Graph 3.

 

Scale    15 ft = 5 cm   so that 1 ft = 0.33 cm

Nn = 38 (number of element using Newmark chart)
 

 

Graph 5.

 

Scale    30 ft = 5 cm   so that 1 ft = 0.167 cm

Nn = 24 (number of element using Newmark chart)
 

Graph 4.

 

Scale    20 ft = 5 cm   so that 1 ft = 0.25 cm

Nn = 33 (number of element using Newmark chart)
 

 

 

 

 

 

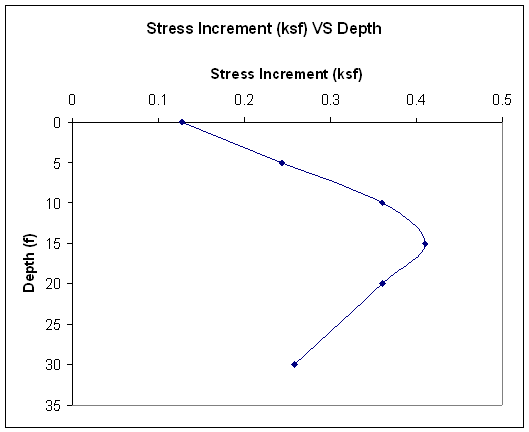
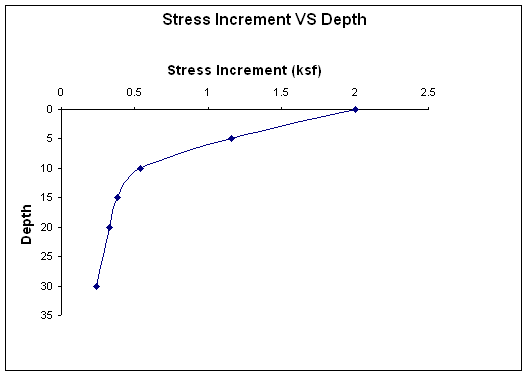
z (ft)

Dsz (ksf)

0

2

5

1.16

10

0.54

15

0.38

20

0.33

30

0.24